単変量線形回帰(単回帰)モデルは学習データ外の値や外れ値で予測した場合
- 意味のない値
- 大きく外れた値
になる可能性があり注意が必要です。ここでは単回帰モデルの予測の留意点、対処法を説明します。
学習データ外での予測の留意点
まず前提として
- 学習データ: [math](x_i, y_i),\ i=1,2,\dots,N[/math]
は[math]x_1=x_2=\cdots=x_N[/math]ではないとします。この時、単回帰モデルは
[math]
y =
\hat{\beta}_0 +
\hat{\beta}_1 x
[/math]
で与えられます。[math]\hat{\beta}_0,\ \hat{\beta}_1[/math]の具体的な値は「基本的な性質」を参照ください。
単回帰モデルは説明変数と目的変数に比例関係があることを仮定しており学習データ外の領域でも比例関係が継続すると仮定します。
学習データ外の値で予測することを「外挿(Extrapolation)」と呼び、誤った結果を含んでいる可能性があるため注意が必要です。
- 説明変数[math]x[/math]: [math]0[/math]〜[math]10[/math]
- 目的変数[math]y[/math]: おおよそ[math]1[/math]〜[math]11[/math]
- [math]x, y[/math]の関係: [math]x[/math]が1増えると[math]y[/math]はおおよそ1減る
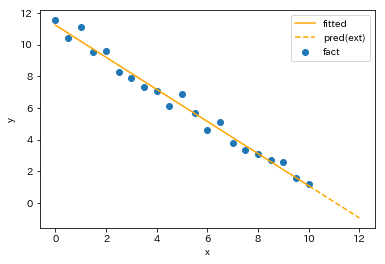
となっており単回帰モデルを構築すると以下の結果が得られます。
図の直線は
- 実線部: 学習データに対する当てはめ
- 点線部: 学習データ外に回帰直線を延長
を示しています。
学習データ外でも予測値を計算できますが目的変数が「長さ」「重さ」など0以上の値をとる場合、負の予測値は意味がありません。他にも売上予測で売上が将来にわたって直線的に伸び続けると予測してしまうなど外挿する場合は
比例関係が継続すると考えるのが妥当か
を吟味する必要があります。
外れ値での予測の留意点
また、外れ値での予測も注意が必要です。[math]\hat{\beta}_1 \ne 0[/math]なので[math]x \to \infty[/math]の時、[math]|y| \to \infty[/math]になり十分大きな[math]x[/math]に対して予測値の絶対値は大きな値になります。したがって、
単回帰モデルの予測値は学習データでの目的変数の値域を大きく超える
ことがあります。外挿と同様に比例関係が続くのかを検討する必要があります。
予測の留意点
以上より、単回帰モデルで学習データ外や外れ値で予測した場合
- 意味のない値
- 大きく外れた値
を出すことがあります。
予測結果を意思決定などに利用する場合は、予測値をそのまま用いるのではなく
- 予測前に説明変数が学習データの範囲内、もしくは比例関係が続くと想定される範囲内かチェック
- 説明変数が範囲外の場合は丸め処理などを行う
- 予測値が目的変数の定義域や意味のある範囲かチェック
- 範囲外の場合は丸め処理などを行う
といった前処理、後処理を検討、設計する必要があります。
シリーズ記事
「機械学習」の「教師あり学習手法」の中で最も基本的な手法として「単回帰」の性質を紹介しています。
誤差項について「無相関で分散一定」「独立同一な正規分布」を仮定するとで様々な性質を導くことができますが、ここでは誤差項について特に仮定せずに導ける性質として
- 考え方と基本的な性質: 回帰係数の導出、回帰直線の性質、計算量との関係
- 決定係数: 決定係数と相関係数の関係
- 予測の留意点(本記事): 学習データ外の値や外れ値で予測する場合の留意点と対処法
- 外れ値の影響: 外れ値が学習時に与える影響
を解説しています。
また単回帰を拡張した「重回帰」でも同様の性質を示せるのでそちらも参照ください。