【統計検定1級過去問】2016年（理工学）大問1

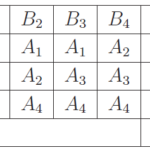
処理[math]A_i(i=1,2,3,4)[/math]を5つのブロック[math]B_j(j=1,\dots,5)[/math]に配置して1回ずつ実験する。

処理[math]A_i[/math]がブロック[math]B_j[/math]で実験した時の観測値を[math]Y_{ij}[/math]としブロック計画モデル

[math]Y_{ij}=\mu+\tau_i+\beta_j+\epsilon_{ij}[/math]

を考える。ここで

• [math]\mu[/math]: 一般平均
• [math]\tau_i[/math]: 処理[math]A_i[/math]の処理効果（[math]\sum_{i}\tau_i=0[/math]）
• [math]\beta_j[/math]: ブロック[math]B_j[/math]の処理効果（[math]\sum_{j}\beta_j=0[/math]）
• [math]\epsilon_{ij}[/math]: 互いに独立な誤差（[math]E[\epsilon_{ij}]=0,\ V[\epsilon_{ij}]=\sigma^2[/math]）

とする時、以下の問に答えよ。

1. [math]T_1=Y_{11}-Y_{21}[/math], [math]T_2=Y_{12}-Y_{22}[/math], [math]T_3=Y_{15}-Y_{25}[/math]は[math]\tau_1-\tau_2[/math]の不偏推定量であることを示せ。また、[math]V[T_1],\ V[T_2],\ V[T_3][/math]を求めよ。
2. [math]Y_{13},\ Y_{33},\ Y_{43},\ Y_{24},\ Y_{34},\ Y_{44}[/math]の線形結合を考え、[math]\tau_1-\tau_2[/math]の不偏推定量かつ分散が最小の推定量[math]T_4[/math]を求め、[math]V[T_4][/math]を求めよ。
3. [math]w>0[/math]として

   [math]T=\dfrac{T_1+T_2+T_3+wT_4}{3+w}[/math]

   が[math]\tau_1-\tau_2[/math]の不偏推定量であることを示し、[math]V[T][/math]を求めよ。さらに[math]V[T][/math]が最小になる[math]w[/math]を求め、その時の[math]T, V[T][/math]を求めよ。

4. 問3で求めた推定量[math]T[/math]の最適性を論ぜよ。