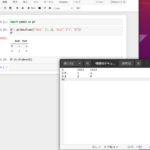
2018年 統計検定1級(統計数理)大問3
確率変数[math]X[/math]は二項分布[math]B(n, \theta)[/math]に従うとする。以下の問いに答えよ。
- [math]E[X],\ V[X][/math]を求めよ。
- [math]X[/math]の条件付き確率[math]h(x)=P(X=x|X\geq 1)[/math]は以下で与えられることを示せ。
[math]
h(x)=\dfrac{_n C_{x} \theta^{x}(1-\theta)^{n-x}}{1-(1-\theta)^{n}} \quad(x=1, \dots, n)
[/math] - [math]\eta(\theta)=E[X | X \geq 1],\ \xi(\theta)=V[X | X \geq 1][/math]を求めよ。
- [math]n=8[/math]の時、[math]\eta(\theta)=2 E[X][/math]となる[math]\theta[/math]を求めよ。
- 問2で求めた条件付き分布からの観測値を[math]y_{1}, \dots, y_{m}[/math]とし、標本平均を[math]\bar{y}=\left(y_{1}+\cdots+y_{m}\right) / m[/math]とする。この時、パラメタ[math]\theta[/math]の最尤推定値[math]\hat{\theta}[/math]の計算法を示せ。また、[math]\hat{\theta}[/math]はモーメント法に基づく推定値でもあることを示せ。
(出典:統計検定HP「統計検定 1級の過去問題」。問題文を一部略記。)
シリーズ記事
- 過去問と解答例
- 2018年(統計数理)大問2
- 2018年(統計数理)大問2 解答例
- 2018年(統計数理)大問3(本記事)
- 2018年(統計数理)大問3 解答例
- 2018年(統計数理)大問5
- 2018年(統計数理)大問5 解答例