【統計検定1級過去問】2019年（理工学）大問1 解答例

コメント

頻出テーマである生存時間解析からの出題でした。生存時間解析では

• 生存時間分布の確率密度関数、累積分布関数
• 生存関数
• ハザード関数

など様々な関数とその関係を押さえておくことが重要です。特に生存関数[math]S(t)[/math]とハザード関数[math]h(t)[/math]には

[math]

h(t) = -\dfrac{S'(t)}{S(t)} = -\dfrac{d}{dt}\log S(t)
[/math]

という関係がありますが初見で思いつくのは難しいので一度、経験していたかがポイントになると思います。

準備していた人には難易度としては難しくなかったと思いますが、量が多いため時間との勝負になったと思います。

問題

（出典：統計検定HP「統計検定 1級の過去問題」。問題文を一部略記。）

問1

まず[math]F(t)=1-S(t)[/math]なので

[math]
\begin{eqnarray}

f(t) &=& \dfrac{d}{dt}F(t) \\
&=& – \dfrac{d}{dt}S(t)
\end{eqnarray}
[/math]

に注意すると、期待値を部分積分して

[math]
\begin{eqnarray}

E[T] &=& \int_0^\infty tf(t) dt \\
&=& \int_0^\infty t \left(- \dfrac{d}{dt}S(t)\right) dt \\
&=& \left[-tS(t)\right]_0^\infty + \int_0^\infty S(t)dt \\
&=& \int_0^\infty S(t)dt
\end{eqnarray}
[/math]

を得る。

問2

問2-1

まず[math]m(t)[/math]は

[math]
\begin{eqnarray}

m(t) &=& E\left[T-t\ |\ T > t\right] \\
&=& \dfrac{\displaystyle\int_t^\infty S(x)dx}{P(T > t)} \\
&=& \dfrac{\displaystyle\int_t^\infty S(x)dx}{S(t)}
\end{eqnarray}
[/math]

と書ける。

問2-2

[math]\dfrac{d}{dt}\log S(t)[/math]を考えると

[math]
\begin{eqnarray}

\dfrac{d}{dt}\log S(t) &=& \dfrac{S'(t)}{S(t)} \\
&=& – \dfrac{f(t)}{S(t)} \\
&=& -h(t)
\end{eqnarray}
[/math]

より[math]h(t)=-\dfrac{d}{dt}\log S(t)[/math]なので累積ハザード関数は

[math]
\begin{eqnarray}

H(t) &=& \int_{0}^t h(s)ds \\
&=& -\log S(t)
\end{eqnarray}
[/math]

とかけ、これより

[math]

S(t) = \exp\left[-H(t)\right]
[/math]

を得る。問2-1の結果とあわせて

[math]
\begin{eqnarray}

m(t) &=& \int_t^\infty \dfrac{S(s)}{S(t)}ds \\
&=& \int_t^\infty \exp\left[H(t)-H(s)\right] ds \\
&=& \int_0^\infty \exp\left[H(t)-H(t+x)\right] dx
\end{eqnarray}
[/math]

を得る。

問2-3

問2-1の結果から

[math]

m(t)S(t) = \displaystyle\int_t^\infty S(x) dx
[/math]

が成立する。両辺を[math]t[/math]で微分すると

[math]
\begin{eqnarray}

&& m'(t)S(t) + m(t)S’t = – S(t) \\
&\Leftrightarrow& \dfrac{S'(t)}{S(t)} = – \dfrac{1+m'(t)}{m(t)}
\end{eqnarray}
[/math]

が成立する。両辺を区間[math][0,\ t][/math]で積分して

[math]

\log S(t) = \displaystyle – \int_0^t \dfrac{1+m'(x)}{m(x)} dx
[/math]

が成立するので

[math]

S(t)=\exp\left[-\displaystyle\int_0^t\dfrac{1+m'(x)}{m(x)}dx\right]
[/math]

が成立する。

問3

問3-1

時刻[math]t[/math]まで稼働し時刻[math][t,\ t+\Delta t][/math]で故障する確率は

[math]

\dfrac{P(t < T < t+\Delta t)}{P(T > t)} = \dfrac{F(t+\Delta) – F(t)}{S(t)}
[/math]

となる。したがって単位時間あたりの故障率は

[math]

\dfrac{F(t+\Delta t) – F(t)}{\Delta t}\cdot\dfrac{1}{S(t)}
[/math]

になり[math]\Delta t\to 0[/math]とすると

[math]
\begin{eqnarray}

\lim_{\Delta t\to 0}
\dfrac{F(t+\Delta t) – F(t)}{\Delta t}\cdot\dfrac{1}{S(t)} &=& \dfrac{F'(t)}{S(t)} \\
&=& h(t)
\end{eqnarray}
[/math]

になる。したがって、ハザード関数[math]h(t)[/math]は時刻[math]t[/math]まで稼働しており、時刻[math]t[/math]で故障する確率を表す。

問3-2

[math]
\begin{eqnarray}
&& 
H(t): 凸関数 \\
&\Rightarrow& H^{\prime \prime}(t)=h'(t) \geq 0 \\
&\Rightarrow& h(t): 増加関数
\end{eqnarray}
[/math]

より寿命分布はIFRである。[math]H(t)[/math]が凹関数の場合も同様に寿命分布はDFRになる。

問4

問4-1

まず[math]T[/math]の累積分布関数は

[math]
\begin{eqnarray}

G_\beta(t) &=& P(T \leq t) \\
&=& P(X \leq t^\beta) \\
&=& 1-\exp\left[-t^\beta\right]
\end{eqnarray}
[/math]

なので

[math]
\begin{eqnarray}

g_\beta (t) &=& \dfrac{d}{dt}G_\beta(t) \\
&=& \beta t^{\beta – 1}\exp\left[-t^\beta\right]
\end{eqnarray}
[/math]

および

[math]
\begin{eqnarray}

h_\beta(t) &=& \dfrac{g_\beta(t)}{1-G_\beta(t)} \\
&=& \dfrac{\beta t^{\beta – 1}\exp\left[-t^\beta\right]}{\exp\left[-t^\beta\right]} \\
&=& \beta t^{\beta – 1}
\end{eqnarray}
[/math]

となる。これより[math]T[/math]の分布のIFR性、DFR性は

• [math]\beta > 1[/math]: IFR
• [math]\beta < 1[/math]: DFR
• [math]\beta = 1[/math]: IFRかつDFR

である。

問4-2

まず[math]h_{\frac{1}{2}}(t)=\frac{1}{2\sqrt{t}}[/math]の概形は以下になる。

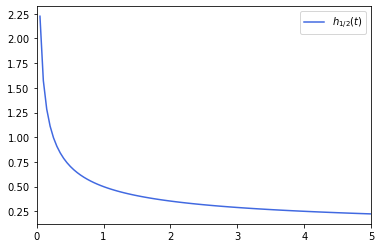
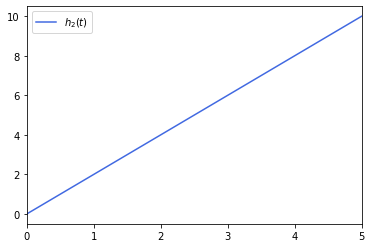
つぎに[math]h_2(t)=2t[/math]の概形は以下になる。

シリーズ記事

• 過去問と解答例
• 2019年（理工学）大問1
• 2019年（理工学）大問1 解答例（本記事）
• 2019年（理工学）大問2
• 2019年（理工学）大問2 解答例
• 2019年（理工学）大問4
• 2019年（理工学）大問4 解答例