コメント
統計的工程管理からの出題でした。伝統的な考え方で管理図を用いると
工程としては問題がないのに管理限界外の点が多発する
という課題に対して考察を行う内容になっています。他の大問と比べかなり易しいのですが、統計的工程管理に馴染みのない人には選択しづらかったと思います。
なお、名古屋工業大学 仁科先生の講演「統計的工程管理の再考」でこの問題が取り上げられており関心のある方は参照ください。
問題
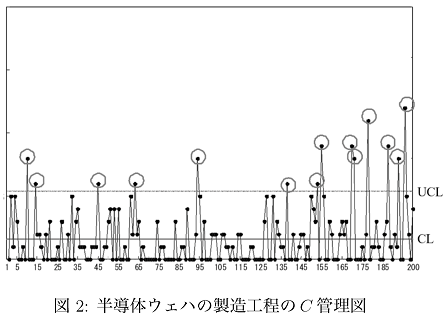
また図2は半導体ウェアのある製造工程におけるウェハ上に付着するパーティクル(微小なゴミ)の数を管理特性とした[math]C[/math]管理図である。管理図は中心線(Center Line)と管理限界線(Control Limit)から成る。管理図のCenter Line(CL)は、管理図に打点される統計量の平均値でありCLの上側にUCL(Upper Control Limit)、下側にLCL(Lower Control Limit)が設定され、
CL [math]\pm[/math] (管理図に打点される統計量の標準偏差) [math]\times 3[/math]
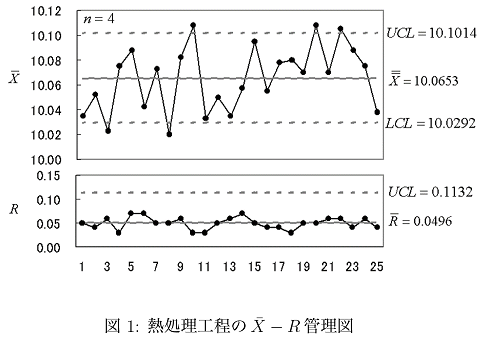
である。[math]\bar{X}-R[/math]管理図での上式における標準偏差は[math]R[/math]管理図によって安定していることを判断した群内変動より求める。標準偏差の3倍で管理限界を設定する方法を3シグマルールという。ただし、[math]R[/math]管理図はLCLが負になる場合は考えない。[math]\bar{X}-R[/math]管理図は正規分布を仮定して作成される。
また、[math]C[/math]管理図はポアソン分布を仮定して作成される。図2のCLは平均値[math]1.62[/math]であり、管理限界線は3シグマルールで計算している。ただし、[math]R[/math]管理図と同様にLCLが負になる場合は考えない。
図1の[math]\bar{X}[/math]管理図および図2の[math]C[/math]管理図ともに管理限界線を越えた点が多発している。この現象に関し以下の問いに答えよ。
(出典:統計検定HP「統計検定 1級の過去問題」。問題文を一部略記。)
問1
群の大きさは4なので管理図に打点される統計量Aの標準偏差は[math]\frac{\hat{\sigma}_W}{\sqrt{4}}[/math]とかける。図1より[math]UCL-\bar{\bar{X}}[/math]は[math]0.0361[/math]なので
[math]
\dfrac{\hat{\sigma}_W}{\sqrt{4}} \times 3 = 0.0361
[/math]
を解いて[math]\hat{\sigma}_W=0.0241[/math]である。
問2
[math]\hat{\sigma}_{\rm Total}^2 = \hat{\sigma}_W^2 + \hat{\sigma}_B^2[/math]より
[math]
\begin{eqnarray}
\hat{\sigma}_B^2 &=& \hat{\sigma}_{\rm Total}^2 – \hat{\sigma}_W^2 \\
&=& 0.0481^2 – 0.0241^2 \\
&=& 0.001733
\end{eqnarray}
[/math]
より[math] \hat{\sigma}_B=0.416[/math]である。
問3
偶然変動を群内変動のみとするのではなく、鋼材によるバッチ間変動も偶然変動とみなす。つまり、[math]\bar{X}[/math]管理図の管理限界線は全変動[math]\hat{\sigma}_{\rm Total}[/math]を用いて設定する。
問4
ポアソン分布の平均を[math]\mu[/math]とした時、分散も[math]\mu[/math]なので
UCL [math]= \mu + 3\sqrt{\mu}=1.62+3\sqrt{1.62}=5.43[/math]
である。
問5
ウェハ上のパーティクルの付着率が一定と仮定しポアソン分布を用いているが、図2の後半で付着数が増加していることから実際は付着率は変動していることが想定される。
つまり、付着率を一定として標準偏差を過少に見積もってしまい管理限界外の点が多発していることが想定される。そのため、付着率は一定ではなくガンマ分布などの確率分布に従うとして[math]C[/math]管理図を活用することが考えられる。
シリーズ記事
- 過去問と解答例
- 2019年(理工学)大問1
- 2019年(理工学)大問1 解答例
- 2019年(理工学)大問2
- 2019年(理工学)大問2 解答例(本記事)
- 2019年(理工学)大問4
- 2019年(理工学)大問4 解答例