【統計検定1級過去問】2019年（理工学）大問1

• 累積分布関数: [math]F(t)=P(T \leq t)[/math]
• 生存関数: [math]S(t)=P(T > t)=1-F(t)[/math]
• 確率密度関数: [math]f(t)=\dfrac{d}{dt}F(t)[/math]
• ハザード関数: [math]h(t)=\dfrac{f(t)}{S(t)}[/math]
• 累積ハザード関数: [math]H(t)=\int_{0}^t h(s)ds[/math]

とする。[math]F(t), H(t)[/math]は適当な回数微分可能であり、[math]E[T]<\infty[/math]とする。この時、以下の問いに答えよ。

1. [math]T[/math]の期待値[math]E[T]=\displaystyle\int_0^\infty tf(t)dt[/math]に対し

   [math]
   
E[T]=\displaystyle\int_0^\infty S(t)dt
   [/math]

   が成立することを示せ。

2. 製品が時刻[math]t[/math]で稼働している時の余命[math]T-t[/math]の期待値を

   [math]
   
m(t) = E\left[T-t\ |\ T > t\right]
   [/math]

   とする。この時、以下が成立することを示せ。

   1. [math]m(t)=\dfrac{\displaystyle\int_t^\infty S(x)dx}{S(t)}[/math]
   2. [math]m(t)=\displaystyle\int_0^\infty \exp\left[H(t) – H(t+x))\right]dx[/math]
   3. [math]S(t)=\exp\left[-\displaystyle\int_0^t\dfrac{1+m'(x)}{m(x)}dx\right][/math]
3. ハザード関数[math]t[/math]が増加関数であるとき寿命分布はIFRであるといい、減少関数のときDFRという。
   1. ハザード関数[math]h(t)[/math]は寿命のどのような性質を意味するか述べよ。
   2. 累積ハザード関数[math]H(t)[/math]が凸関数のとき寿命分布はIFRであり、凹関数のとき寿命分布はDFRになることを示せ。
4. 確率変数[math]X[/math]はパラメタ1の指数分布に従うとする。[math]X[/math]の累積分布関数は[math]F(x)=1-e^{-x}[/math]である。[math]\beta > 0[/math]を用い[math]T=X^{1/\beta}[/math]と変数変換する。
   1. [math]T[/math]の確率密度関数[math]g_\beta(t)[/math]、ハザード関数[math]h_\beta(t)[/math]を求め、[math]\beta[/math]の値と[math]T[/math]の分布のIFR性、DFR性との関係を示せ。
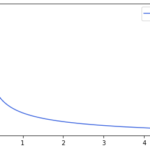
   2. [math]\beta=\frac{1}{2}, 2[/math]とした時のハザード関数[math]h_{\frac{1}{2}}(t), h_2(t)[/math]を求め[math]0 < t < 5[/math]でそれぞれの関数の概形を図示せよ。