週記(23/05/14)：拡張整数ライブラリ

今週のまとめ

• 拡張整数ライブラリを作った
• ABC302は久々の6完！も青復帰にはギリギリ届かず

です。

(本文中にABC 287 E, 302 D-Gの解法を含む話題が出てくるのでご注意ください。)

5/15(Mon)

この日は夜に時間ができたのでABC287「E – Wish List」を本腰入れて解きました。

商品[math]i[/math]をどこで回収するかは後続で回収必須な商品の個数によって変わるのでなかなか捉えづらいですね。商品[math]i[/math]より前に回収する商品数を[math]b[/math]とすると回収する場所は

[math]
\min_{i-b \leq j \leq i} C_j
[/math]

を達成できる場所なのでdp[i][b][f]を

[math]i[/math]個目まで見て回収する商品数を[math]b[/math]として[math]i[/math]を回収する/しない場合の最小コスト

とすると遷移式が導けます。必ず買う商品は[math]f=0[/math]のコストを無限大にすればOKです。

サンプルもすんなり通ってSubmitするとなんとMLE!

3次元vectorだと1.7GBくらい消費してしまうようで1次元化するか生配列にすると400MBくらいになって通りました。vectorはオーバヘッドが大きいんですね。

5/17(Wed)-19(Fri)

今までに幾度となくオーバーフローに苦しんでて^[1]ABC301 Eもオーバーフローで1WAに苦しんだ。

「オーバーフローに気を付ける」だけだと限界がある

ので仕組みでなんとかしようと思い拡張整数？とでも呼ぶクラスを作りました。

仕様としては単純で

• long long型をラップ
• long long型の最大値を[math]+ \infty[/math], 最小値を[math]-\infty[/math]に対応付ける
• 加減算を無限に丸める(ex. [math]a \pm \infty = \pm \infty[/math])
• 乗算も無限に丸める(ex. [math]c \times \pm \infty = \pm \infty(c > 0)[/math])

です。よくあるミスの

番兵値にlong longの最大値を設定^[2]もちろん問題ごとに最大値より小さな番兵値を適切に設定するのも手ですが極力、考察が必要な要素を減らしたいです。。最大値チェック漏れで加算しオーバーフロー

を防げます。これがオーバーフローバグの切り札になればよいのですが。

5/20(Sat)

ABC302の参加

2か月半ぶりに6完(65分)と上々な結果！パフォ1676で青に復帰できるかと思いましたが1599でギリギリ復帰ならず…。

「D – Impartial Gift」は最初贈り物が「1つずつ」を見落として悩みましたが1つだけだと[math]B_j[/math]をソートしておいて[math]A_i[/math]ごとに「[math]A_i+D[/math]以下の最大の[math]B_j[/math](ただし、[math]A_i-D[/math]以上)」を求めればOK。

「E – Isolation」は次数と隣接リストをsetで管理してシミュレーション。1本も辺がない頂点に対して辺削除があることを見落としてましたがサンプル2に助けられました。

「F – Merge Set」は集合番号と数字の対応表をサンプル4で描くと

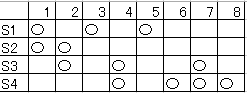
になって数字1を含む集合を選ぶ⇒集合の数字を選ぶ⇒数字を含む集合選ぶを繰り返して[math]M=8[/math]まで行けるか？と言い換えられて二部グラフの最短路になります。

すべての頂点、辺を持つとTLEですがBFSしながら必要な要素だけ持てば通ります。

本番はFまで解けたことに満足しGをぼーっと考えているうちに終わったのですが、実は通すだけなら可能性があった^[3]貪欲法で解ける問題だったので終わるまで気を抜かないことが大切ですね。

関連記事

• 前週の週記: 「ゴールデンウイーク」
• 翌週の週記: 「七五三」