1.4. 条件付き確率と事象の独立

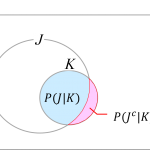
これまでは標本空間[math]S[/math]の部分集合に対して確率を定義しました。新しい情報が得られた場合に標本空間、事象を取り直して確率を評価するのが条件付き確率(conditional probability)です。まず定義を紹介します。

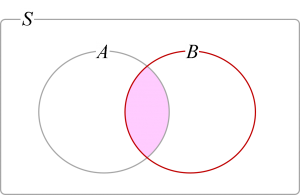
事象[math]B[/math]（下図赤線部）を全事象とみなした時に[math]A, B[/math]が同時に生じる事象（下図薄赤部）の確率が条件付き確率です。

実際に[math]P(\cdot | B)[/math]はコルモゴロフの公理を満たすので確かに確率関数になっていることがわかります。 有名な問題^[1]2人の子供問題(Boy or Girl paradox)として知られています。詳細はこちら。でその考え方を見てみましょう。

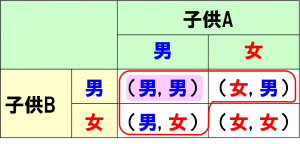
2人の子供を子供A, 子供Bとすると2人の性別の全組合せは下図の通り4通りあります。

事象[math]A, B[/math]をそれぞれ

• [math]A=\{[/math]2人とも男の子[math]\}[/math]
• [math]B=\{[/math]少なくとも1人は男の子[math]\}[/math]

とおくと[math]A[/math]は上図の薄赤部、Bは赤線部になります。[math]P(A\cap B)=1/4, P(B)=3/4[/math]より求める確率

[math]
P(A|B)=\dfrac{1/4}{3/4}=1/3
[/math]

が得られます。何も事前情報がないと2人とも男の子である確率は[math]P(A)=1/4[/math]ですが、少なくとも1人は男の子という情報を得ることで[math]P(A|B)=1/3[/math]と少し確率が上がることがわかります。

逆にある事象[math]B[/math]が生じたという情報を得ても事象[math]A[/math]の条件付き確率が変化しない、つまり

[math]
P(A|B)=P(A)
[/math]

となることもあります。この時、条件付き確率の定義式から[math]P(A)=P(A|B)=\dfrac{P(A\cap B)}{P(B)}[/math]となり

[math]
P(A\cap B)=P(A)P(B)
[/math]

という関係が成立します。さらに

[math]
\begin{eqnarray}
P(B|A) &=& \dfrac{P(A\cap B)}{P(A)} \\
&=& \dfrac{P(A)P(B)}{P(A)} \\
&=& P(B)
\end{eqnarray}
[/math]

なので事象[math]A[/math]が起きたという情報は事象[math]B[/math]の確率に影響を与えないことがわかります。この互いの確率に影響を与えない関係を「事象の独立」と呼び定義は以下になります。

2つの事象が独立なら事象間の相互作用を考慮する必要がなくそれぞれの事象の確率を求めることで同時確率が得られます。状況をよりシンプルに解析することができ、中心極限定理など重要な定理の証明でもこの独立性が大きな役割を果たします。

また、独立ではない事象間の条件付き確率は時に「直感的に正しいと思える答え」と「論理的に正しい答え」が異なることがあり理解しづらい分野の一つです。次の記事では条件付き確率を計算する際に有用な「ベイズの定理」とその応用例を紹介したいと思います。

シリーズ記事

• 統計学
  • 1.3 確率の基本的性質
  • 1.4 条件付き確率と事象の独立(本記事)
  • 1.5 ベイズの定理

参考文献

• Casella, G and Berger, R.L.(1990), Statistical Inference(Second Edition): Section 1.3 Conditional Probability and Independence