前回の記事「1.6 確率変数」では確率変数[math]X[/math]の振る舞いを解析するために累積分布関数
[math]
F_X(x)=P(\{s\in S\ |\ X(s)\leq x\})
[/math]
を導入しました。累積分布関数は[math]X(s)\leq x[/math]となる事象の確率に着目していますが、ここでは[math]X(s) = x[/math]となる事象の確率に着目し累積分布関数との関係を調べます。
確率質量関数
確率変数[math]X[/math]が離散型の場合、次で定義される関数を確率質量関数(probability mass function, pmf)と呼びます。
[math]
f_X(x) = P(X = x)
[/math]
例えば確率変数[math]X[/math]を「10回サイコロを投げた際の1が出た回数」とすると
[math]
f_X(x) = P(X = x) = {}_{10}C_{x} (1/6)^{x}(5/6)^{10-x}
[/math]
となります。
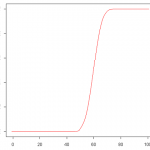
また、累積分布関数[math]F_X(x)[/math]は確率質量関数を使って
[math]
\begin{eqnarray}
F_X(x) &=& P(X\leq x) \\
&=& \sum_{k \leq x} f_X(k)
\end{eqnarray}
[/math]
と書けます。
確率密度関数
確率変数[math]X[/math]が連続型の場合は点[math]X=x[/math]となる確率は
[math]
\begin{eqnarray}
P(X = x) &\leq& P(x-\varepsilon < X \leq x) \\
&=& F_X(x) - F_X(x-\varepsilon) \\
&\to& 0 \quad (\varepsilon \to 0)
\end{eqnarray}
[/math]
と常に0になってしまい解析に役立つ形で定義できません。そこで離散型での関係式
[math]
F_X(x) = \sum_{k \leq x} f_X(k)
[/math]
に対応する関数を定義し、確率密度関数(probability density function, pdf)と呼びます。
[math]
F_X(x) = \displaystyle\int_{-\infty}^x f_X(t)dt
[/math]
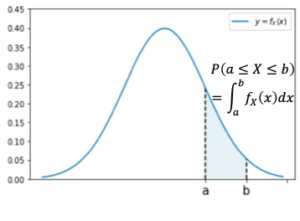
確率密度関数を用いると確率変数[math]X[/math]が区間[math][a, b][/math]に入る確率は
[math]
P(a \leq X \leq b) = F_X(b) – F_X(a) = \displaystyle\int_{a}^b f_X(t)dt
[/math]
と書けます。つまり[math]y=f_X(x)[/math]を描いたときの区間[math][a, b][/math]における面積が確率に対応します。
また確率密度関数[math]f_X(x)[/math]が連続の場合、微分積分学の基本定理より
[math]
f_X(x) = \dfrac{d}{dx} F_X(x)
[/math]
が成立します。
最後に与えられた関数[math]f_X(x)[/math]が確率密度関数になるための必要十分条件を紹介します。
- [math]f_X(x) \geq 0[/math]
- [math]\displaystyle\int_{-\infty}^\infty f_X(x)dx = 1[/math]
関数[math]f_X(x)[/math]が確率密度関数の場合、
- [math]f_X(x) \geq 0[/math]
- [math]\displaystyle\int_{-\infty}^\infty f_X(x)dx = 1[/math]
であることは定義から容易に示せます。
逆に関数[math]f_X(x)[/math]が2条件を満たす場合、[math]F(x) := \displaystyle\int_{-\infty}^x f_X(t)dt[/math]と定義すると
- [math]\lim_{x\to-\infty}F(x)=0[/math] かつ [math]\lim_{x\to\infty}F(x)=1[/math]
- [math]F(x)[/math]は[math]x[/math]の非減少関数
- [math]F(x)[/math]は右側連続、つまり任意の[math]x_0[/math]に対し[math]\lim_{x\downarrow x_0}F(x)=F(x_0)[/math]
を満たします。「1.6 確率変数」で紹介した定理から[math]F(x)[/math]は累積分布関数になり、[math]f_X(x)[/math]は確率密度関数になることがわかります。
シリーズ記事
参考文献
- Casella, G and Berger, R.L.(1990), Statistical Inference(Second Edition): Section 1.7 Density and Mass Functions