2016年 統計検定1級(理工学)大問3
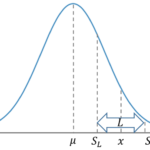
ある製品の特性値が[math]\mathcal{N}(\mu, \sigma)[/math]従うとし、
- 下側規格:[math]S_L[/math]
- 上側規格:[math]S_U[/math]
とし区間[math](S_L, S_U)[/math]を外れた場合は不良品とする。工程能力指数[math]C_p[/math]を
- 母標準偏差[math]\sigma[/math]が既知:[math]C_p=\dfrac{S_U-S_L}{6\sigma}[/math]
- 母標準偏差[math]\sigma[/math]が未知:[math]\hat{C}_p=\dfrac{S_U-S_L}{6S}[/math]
とする。ここで、[math]X_1,\dots,X_n[/math]を無作為標本とし
- 標本平均:[math]\bar{X}=\dfrac{1}{n}\sum_{i=1}^nX_i[/math]
- 標本標準偏差:[math]S=\sqrt{\dfrac{1}{n-1}\sum_{i=1}^n(X_i-\bar{X})^2}[/math]
とする時、以下の問に答えよ。
- [math]\sigma[/math]が既知かつ一定値で[math]S_L,\ S_U[/math]が与えられた時、平均[math]\mu[/math]が[math]\frac{S_L+S_U}{2}[/math]に一致するときに不良率は最小になることを説明せよ。
- 問1の条件下で[math]C_P=\frac{2}{3}[/math]の時の不良率を求めよ。
- [math]\sum_{i=1}^n(X_i-\bar{X})^2/\sigma^2\sim \chi^2(n-1)[/math]を用いて[math]C_P[/math]の信頼係数[math]95\%[/math]の信頼区間が
[math]\left(\hat{C}_P\sqrt{\dfrac{\chi^2_{0.975}(n-1)}{n-1}},\ \hat{C}_P\sqrt{\dfrac{\chi^2_{0.025}(n-1)}{n-1}}\right)[/math]
となることを示せ。なお[math]\chi^2_\alpha(\nu)[/math]は自由度[math]\nu[/math]のカイ二乗分布の上側[math]100\alpha\%[/math]点である。
- [math]S_L=12.0[/math]cm, [math]S_U=12.6[/math]cmである製品について考える。20個の製品特性を求めたところ標本標準偏差は0.05cmであった。この時、以下の問に答えよ。
- [math]\hat{C}_P[/math]を求めよ。
- [math]C_P[/math]の信頼係数[math]95\%[/math]の信頼区間を求めよ。
- [math]C_P\geq 1.33[/math]が望ましいとした時、この工程の管理状態を解釈せよ。
- [math]E[\hat{C}_P] / C_P[/math]を求めよ。ただし、[math]\chi^2(\nu)[/math]の確率密度関数は
[math]f(y)=\dfrac{1}{2\Gamma(\nu/2)}\left(\dfrac{y}{2}\right)^{\nu/2-1}e^{-y/2}[/math]
であることは既知として良い。
(出典:2016年受験時の問題冊子。問題文を一部略記。)
シリーズ記事
- 過去問と解答例
- 2016年(理工学)大問1
- 2016年(理工学)大問1 解答例
- 2016年(理工学)大問3(本記事)
- 2016年(理工学)大問3 解答例
- 2016年(理工学)大問4
- 2016年(理工学)大問4 解答例