estieプログラミングコンテスト2022(AHC014)参加記

2022年9月17日～10月1日で開催された「estieプログラミングコンテスト2022(AHC014)」に参加して84位になることができました。

結果は自己最高の順位でしたが今回の問題は

• 良さそうなアプローチ、アイディアを見つけるのが難しかった
• アイディアを実装して良いスコアに結び付けるのが難しかった

という印象で後半に試したアイディアはことごとくお蔵入りになってしまいました。

正直、提出解法に含めなかった内容の方が多いのでこの参加記では

• 試行錯誤したがうまく行かなかったこと
• 他の参加者のやり方を参考にどうすれば良かったのか

を中心に振り返りたいと思います。

なお、参加振り返りで長くなったので日記は別記事化しました。この記事では書けませんでしたが可視化やOptunaによるチューニングについても触れています。

コンテスト／問題概要

[math]N \times N(31\leq N \leq 61)[/math]の格子点上に[math]M(N\leq M \leq N^2/12)[/math]個の点が与えられます。ここから3点を選んで以下の条件を満たす長方形を作っていきます。

• 長方形の向きは座標軸に平行か45°回転
• 長方形を作るときに他の点を通ってはいけない
• 他の長方形と辺を共有してはいけない

点ごとに「中心点からの二乗距離+1」のスコアが与えられ、スコアの合計を最大化する問題になります。

提出解法

焼きなまし法で求めました。状態として「長方形の作成手順」を持って遷移は

• ランダムに1～3個の長方形を追加
• ランダムに長方形を削除
  • 削除によって作れなくなる長方形も一緒に削除
  • 削除した個数に比例してランダムに長方形を追加し直す

を行いました。

実はこれしかやっていません。これを時間いっぱい回すだけで平均スコア900K(暫定テストで45M相当)を出すことができて、これに

• 焼きなまし法1回あたりの最大反復回数
• スコア更新が一定回数ない場合に打ち切る

をチューニングして焼きなましを複数回行い一番良いものを出力すると平均スコア960K(暫定テストで47M相当)まで伸びました。

必要最低限な遷移しか考えていませんが手元の10,000ケースの中では最大で1,920,093点取ることができました。(seed=3343)

狙ってこの解法にたどり着いたわけではなく参加中は色々と遷移の仕方や他の探索との合わせ技を考えたのですがことごとく性能改善につながらなかったです。

結果的に最低限必要な遷移を高速に回す「量で質を生み出す解法」になりました。

実装での工夫

長方形の生成

「生成可能な長方形」を高速に求めるため各格子点で以下の情報

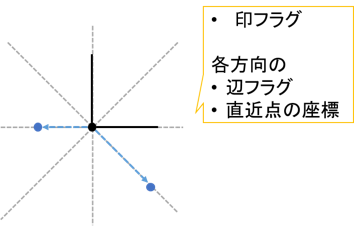
• 点フラグ
• 8方向ごとの
  • 辺フラグ
  • 直近点の座標

を持ちました。

長方形の生成は印のある点Pから長方形を作れる方向（90°の2辺、ただし辺を出していないこと）を見ていき、直近点Q, Rが分かれば新しくできる点Sも分かります。

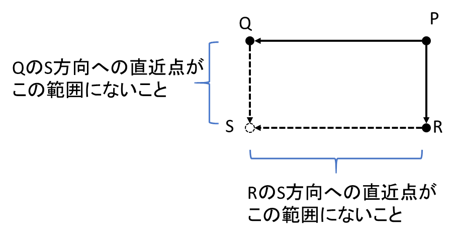
Q,RはPから見た直近点なので辺PQ, PR上に他の点はありません。QS, RS上に点がないかはRから見たS方向の直近点との距離とSまでの距離を比較して判定することができます。さらに他の長方形と辺を共有していないかもQ, Sの辺フラグで判定できます。

また、生成可能な長方形は頂点とその頂点から出る辺の向きと1対1対応するので上記の処理を既存の点について行うと生成可能な長方形を網羅できます。計算量は既存の点数を[math]K[/math]として[math]O(K)[/math]で済みます。

さらに今回は長方形のランダム生成しか行わなかったので生成可能な長方形リストは保持せず生成済みの点Pをランダムに選んで長方形を[math]O(1)[/math]で生成しました。まとめて複数個を生成する際も盤面は更新せずランダム生成した長方形が競合しないかをチェックするようにしました。

細かな高速化のポイントとしては座標[math](x,y)[/math]をそのまま持つのではなく[math]64x+y[/math]と一次元化して64 x 64の固定配列で持つようにしました^[1]vectorを使ってN x Nの2次元配列で持つのと比べて5%ほど高速化しました。。他にも各点で持つ情報を64bit変数で持つとより省メモリ化＆高速化しますが今回はそこまでは手が回りませんでした。

焼きなまし法での遷移判定

焼きなまし法では現在の状態[math]s[/math]から次の状態[math]s'[/math]を生成してスコアの差分[math]S_d[/math]を計算して遷移するかどうかを決めます。

長方形を削除する遷移を選んだ場合、「削除によるスコアの減少＋ランダム追加の増加」を計算する必要がありますがざくっと「削除によるスコアの減少分 x (一定割合)」と概算値で遷移するかを決め、遷移する場合に計算し直すようにしました。大きく削除するケースは遷移しない可能性が高いので概算でその判定をして高速化しました。

参加中の試行錯誤と振り返り

ここからはお蔵入りになってしまったアイディアを中心に他の参加者の方の解法を参考にこうしておけば良かった…と振り返りたいと思います。

辺、隅の位置を決め打ってその場所への置き方を探す

スコアの定義上、中心⇒辺⇒隅へと行くほど点数が上がるので辺や隅の狙った場所に置くことを繰り返せないか？と考えました。

例えば右上の隅の場所を１つ決め打ってそこに置くのに必要な長方形の場所の候補が直線上に決まって、さらにその候補を作るには…と再帰的に探索を行います。

実装してみると辺の領域なら求められるのですが、1点へのパスを求めるのに結構時間がかかるのと隅へのパスを求めるのは難しそうだったので断念しました。

「賢い」乱択を行う

長方形を追加する際に「置いて良さそうな長方形」をうまく選ぶことで探索性能を上げられないか？と思ったのですが、「置いて良さそう」の判断基準がまったく分からず結局最後までランダム選択のままでした。

作問者であるwataさんの解説動画を見ると

• 辺を共有できないので小さく作って徐々に広げるのが良い
• たくさん点を作った方が良いので各点から8方向すべてに辺が出る(4つの長方形に属する)のが良い。各点4枠あるとして
  • 新しい点が空白なら全体として枠が減っていない⇒どんどん長方形を作れる可能性あり
  • 新しい点が他の長方形の辺上だと残り枠がすでに1で損

と考察をされていてて、その考察に基づいたRandom playoutを構成^[2]これで50Mを越えるようで正しい考察をもとにロジックを組むと複雑なことをしなくても十分高性能なものが作れる好例ですね。されていてなるほどなぁ…と感心しきりでした。

長方形の置く場所や辺の出方は考えたのですが、各点に4枠あってどうすれば枠を無駄遣いせずに大きくできるか…という発想はなかったですね。

マクロな理想状況からミクロでどういう状況が良いのか？を落とし込むのは難しいですが、ヒラメキに頼るのも辛いので丁寧に言語化することを繰り返してうまくできるようになりたいですね。

探索アルゴリズム

前半1週間で乱択、貪欲法を試して「序盤の配置が良かったかは最後、作り切ってみないと分からない」と思いました。方針としてビームサーチは難しい^[3]序盤で上位K個に入ることとと最終的な良さと関連が薄そうなため。ので優先度を下げ、MonteCarlo Tree Search(MCTS)か焼きなまし法か遺伝的アルゴリズムで迷いました。

MCTSは過去に経験がありあまりコンペでは見ないので、これがハマって上位になれば気持ち良いだろうなぁという欲を大いに感じつつも

• 制限時間が5秒しかない
• 序盤は候補長方形が数十個以上あり候補が非常に多い
• 良い手順を見極められないまま中途半端な状態で探索が終わる懸念

がありぐっとこらえました。遺伝的アルゴリズムは経験がなかったのと焼きなまし法なら賢く山登ってそんなに悪いことにはならないだろうと思い焼きなまし法にしました。

コンペ後のTwitterを見ているとビームサーチ、MCTSでも良い結果を出している方がいたので参加記を拝見しようと思います。

「良い」配置を目指す

スコアが良かったサンプルを確認すると辺の領域へ三角形状に伸ばしていくことができているものが多いです。

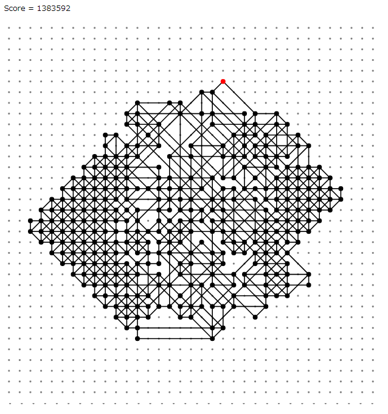
良く見ると「ある辺の出方をした点が2列並ぶ」（「良い」配置とします）と連鎖的に長方形を外側に作っていくことができます。

この観察から

• 「良い」配置を目指すパート
• 「良い」配置から外側に伸ばすパート

に分けて解くとかなりの高得点が出せるのでは？と考えました。

この考察、読みは当たっていたようでトップ層は同じ考えをされていたようです。

ただ、

• 「良い」配置は初期配置の外枠付近に作れると良いけど、外枠ギリギリに作れるかはわからない
• 「良い」配置をどこまで長くできるかは分からない

と思って焼きなまし法の評価関数で評価して探索しましたが

• 小さな「良い」配置がたくさんできるが小さいため大きくは伸びない
• 「良い」配置探索中から一部、外側を作ってしまい後続の伸ばすロジックがうまく動かなくなった

という結果になりうまくいきませんでした。

他の参加者でうまく実現できていた方は

• 「良い」配置を作る場所は初期配置の外枠に固定
• 外枠に置くときは辺の条件を満たすもののみ置く
• 初期配置の外側には置かない

と場所の決め打ちと制約条件として制限をかけた探索をされていました。

焼きなまし法で行く場合は何を状態として持ち、遷移として何を認めて、逆に制限として何を認めないかがポイントで、今回はやりたいことを実現する焼きなまし法をうまく設計できなかったですが、これを参考に次回はうまく設計できるようにしたいです。

他の点を通る長方形の生成と手順修正

VisualizerのManual modeで長方形を作っていると先に作った長方形が邪魔で長方形が作れないことがよくあります。ただ、手順を替えることで作れることがあります。

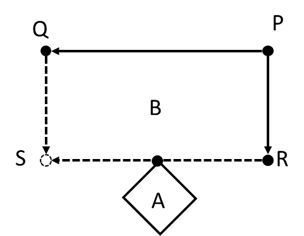
例えば長方形Aの後にBを作ろうとすると点R, S間に点があるため作れませんが、Bの後にAを作ることは可能です。

これは長方形間の先行関係を有向グラフで表現してトポロジカルソート順に並べ替えることができれば先行関係を満たした手順になっています。

さらに閉路があり手順が作れない場合も閉路中の長方形を削ることで有効な手順が作れます。

コンテスト期間のラスト２日の大半をこれにつぎ込んでデバッグもかなり苦労^[4]終盤に高速化のためコンピュータに優しく人には厳しいデータ構造に変えていたこともデバッグが難しくなった要因でした。して実装したのですが、

速度が5割遅くなりスコアはほぼ同じ

という大変残念な結果になりました。なかなか諦めきれなくて確率的に実行する、焼きなましの2回目は実行して多様性を出す…など試したもののすべてスコアが1割以上下がる結果になって泣く泣く最終提出からは外しました。

今、冷静に考えると

• スコアの高い手順は大きさ1の長方形を連鎖的に作っていくことが多い
• 大きさ1の長方形が他の点を通ることはなくそもそも手順前後は発生しない

のでスコア向上にあまり寄与しなかったのだと思います。

「良い」配置を探すパートがうまく行っていればそちらでは有効だったかもしれませんが、評価スコア最大化で動く焼きなましには無用な長物でした。

感想

今回は良いアプローチが見えづらく、また考えたアイディアもなかなかスコア向上につながらず問題の難しさを味わった2週間でした。

ラストの3-4日はやれどもやれどもアイディアがすべて空振りに終わりうまく行かなかったと思いましたが、振り返ってみると

• 前半の乱択、貪欲での結果から妥当な探索方針を決められた
• 「良い」配置から外側に大きくするのがポイントなのには気づけた
• そのアイディアを実現する設計ができなかった

で、ちょっと惜しかったなーという気持ちになっています。

今回も2週間どっぷりAHCに向き合うことができました。日記編で書こうと思いますが、仕事や生活と両立しながら楽しく参加できたと思います。

また、終了後の解説動画、他の方のTweetや参加記もすごく参考になりました。スポンサーのestieさん^[5] … Continue reading、作問者のwataさん、参加者の皆様ありがとうございました！