【統計検定1級過去問】2019年（統計数理）大問4

[math]
f_\theta(x) = \dfrac{1}{\pi\left\{1+(x-\theta)^2\right\}} \quad (-\infty < x < \infty) [/math]

この分布から大きさ1の標本[math]X[/math]に基づき

• 帰無仮説: [math]\theta=0[/math]
• 対立仮説: [math]\theta=1[/math]

に対して検定したい。ここで、棄却域を[math]R = \left\{x | 1 < x < 3\right\}[/math]とする検定を考える。この時、以下の問いに答えよ。ただし、[math]\tan^{-1} 2=1.107[/math], [math]\tan^{-1} 3=1.249[/math], [math]\pi=3.1416[/math], [math]\frac{d}{dx}\tan^{-1}x = \frac{1}{1+x^2}[/math]を用いて良い。

1. この検定のサイズ（第一種の過誤確率）[math]\alpha[/math]を小数第3位まで求めよ。
2. この検定の検出力[math]1-\beta[/math]（[math]\beta[/math]: 第二種の過誤確率）を小数第3位まで求めよ。
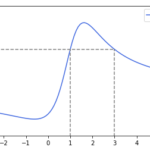
3. 尤度比[math]\lambda(x)=\dfrac{f_1(x)}{f_0(x)}[/math]の[math]x=1[/math]と[math]x=3[/math]における値と[math]\lambda(x)[/math]の概形を描け。
4. この検定はサイズ[math]\alpha[/math]を有意水準とする検定の中で最強力検定になることをネイマン・ピアソンの基本定理を用いて示せ。