パッと思いつく方法は計算量が[math]M![/math]あり制限時間内に解くのは不可能に思える問題が「ぬいぐるみの整理」(JOI 2017 予選4として出題)です。
注意深く考察すると集合に関する部分問題に分解できBit DPと呼ばれる手法で解くことができます。
類題の経験がないと難しく精選100問で初めてBit DPに出会った…という方の中にはかなり苦労した方もいるのではと思います。実際、私も最初この問題を解いた時はBit DPを知らず2時間以上かけてメモ化再帰で解きました。
ここでは復習を兼ねて考察の流れをまとめたいと思います。
問題概要
[math]M[/math]種類のぬいぐるみ[math]N[/math]個が一列に並べられている。同じ種類のぬいぐるみが連続して置かれるように並び替える際に取り出すぬいぐるみの個数の最小値を求めよ。
制限
- [math]1 \leq N \leq 10^5[/math]
- [math]1 \leq M \leq 20[/math]
- 実行時間制限は10秒
考察
まず初期状態として4種類のぬいぐるみ9個が以下のように並んでいたとします。

これを仮に1, 2, 3, 4の順に連続して並べるとします。

この並び替えに必要な取り出し回数は最終状態と初期状態を比較して異なる種類のぬいぐるみを取り出せばよいので
- 1の整理: 1回
- 2の整理: 0回
- 3の整理: 2回
- 4の整理: 1回
の合計4回になります。ぬいぐるみを取り出す必要があるかは
位置ごとに初期状態と最終状態を比較し異なる場合のみ取り出す
で判定できるのが一つ目のポイントです。
次に取り出す回数の最小化を考えます。愚直には[math]M![/math]通り調べれば良いですが[math]M \leq 20[/math]のためこのままでは制限時間内に間に合いません。
一度、部分問題として3種類(1, 2, 4)を並び変える際にうまく問題を分解できないかと考えてみます。(このあたりの発想がDPの経験を積まないと難しいかもしれません。)
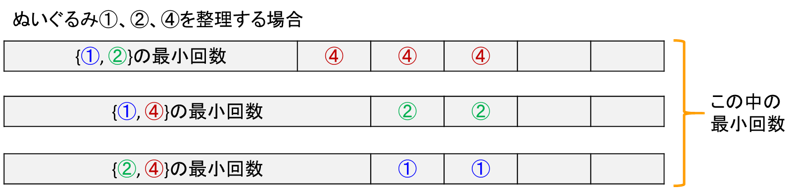
この場合、最後に整理する種類で場合分けすると
- {1, 2}を整理した後に4を整理
- {1, 4}を整理した後に2を整理
- {2, 4}を整理した後に1を整理
の3通りに場合分けができ、この中で取り出し回数最小のものが解になります。ここで重要なポイントとして
先に整理する種類の並び順は不要でその集合が分かれば十分
です。例えば最後に4を整理する場合に1, 2を並べた時の最小回数と「1, 2を並べた」という情報さえあれば取り出し回数を求めることができます。
これに気づけば管理する状態が[math]2^M \leq 2^{20}\approx 10^6[/math]になり光が見えてきます。
これを一般化すると集合[math]S[/math]を
[math]
S = \left\{ j | 種類jは整理済 \right\}
[/math]
として
[math]{\rm dp}[S] = [/math](ぬいぐるみ[math]j \in S[/math]を整理するのに必要な取り出し回数の最小値)
と定義すると
[math]{\rm dp}[S] = \min_{j \in S}\left( {\rm dp}[S \backslash \{j\}] + {\rm pull}(S \backslash \{j\}, j) \right)[/math]
となります。ここで[math]{\rm pull}(X, j)[/math]はぬいぐるみ[math]i \in X[/math]まで整理した状態でぬいぐるみ[math]j[/math]を整理するのに必要な取り出し回数を表し、上で見たようにぬいぐるみ[math]j[/math]を配置する位置と初期状態を比較することで求められます。
最後のポイントが[math]{\rm pull}(X, j)[/math]の計算量で愚直に初期状態と比較すると種類[math]j[/math]のぬいぐるみの個数分の比較が必要です。平均[math]N/M[/math]個ありDPの更新1回につき[math]O(N/M \times M)=O(N)[/math]の計算量がかかり[math]S[/math]の状態が[math]2^M[/math]通りあるので全体で[math]O(N2^M)\approx 10^{11}[/math]となりこれだと間に合いません。
[math]{\rm pull}(X, j)[/math]は「初期状態で区間[l, r)に含まれるぬいぐるみ[math]j[/math]の個数」が分かれば良いので種類ごとに累積和を事前計算([math]O(MN)[/math])して持っておけば[math]O(1)[/math]で求まります。
これでようやく全体の計算量が[math]O(M (2^M + N))[/math]になり制限時間に間に合います。
実装
実装はBit DPと呼ばれる方法が慣れると簡明です。まず集合[math]S[/math]を
[math]j \in S \Leftrightarrow [/math]32ビット変数[math]s[/math]の右から[math]j[/math]ビット目が1
と32ビット変数と対応付けます。
後は[math]s[/math]を0(空集合[math]\emptyset[/math]に対応)から順に[math]2^M-1[/math](すべての種類を整理済)まで増やしていくと集合[math]S[/math]の任意の部分集合[math]S’ \subset S[/math]に対応する32ビット変数[math]s'[/math]は必ず[math]s’ < s[/math]になりsを順次大きくながら更新していけばDP式の右辺は常に計算済みになり正しく遷移を計算することができます。 上記を実装したコードはこちらになります。