ガウス・マルコフの定理：単回帰モデルでの証明

今までは学習データ[math](x_i,\ y_i)[/math]に確率的な仮定を置かず回帰直線の当てはめを考えましたが、ここからは確率的な誤差項を含むモデルを考えます。

[math]
Y_i = \beta_0 + \beta_1 x_i + \varepsilon_i
[/math]

ここではガウス・マルコフの定理として知られる「最小二乗推定量[math]\hat{\beta}_1[/math]」が「最良線形不偏推定量（Best Linear Unbiased Estimator, BLUE）」になることを示します。

なお、重回帰モデルでも同様の結果を示すことができます。詳細は「ガウス・マルコフの定理：重回帰モデルでの証明」を参照ください。

確率モデル

ここでは目的変数[math]Y_i[/math]と説明変数[math]x_i[/math]の間に

[math]
Y_i = \beta_0 + \beta_1 x_i + \varepsilon_i,\quad i=1,\dots,N
[/math]

の関係があり誤差項[math]\varepsilon_i[/math]について以下が成立するとします。

• 平均: [math]E[\varepsilon_i]=0[/math]
• 等分散性: [math]V[\varepsilon_i] = \sigma^2[/math] ([math]\sigma^2[/math]は未知)
• 無相関性^[1]ここでの議論は無相関性を仮定すれば成立し、独立性の仮定は不要です。: [math]Cor[\varepsilon_i, \varepsilon_j]=0\ (i\ne j)[/math]

確率変数[math]Y_i[/math]の観測値を[math]y_i[/math]とします。確率モデルは何が確率変数で何が確定値なのかわかりにくいのでまとめると

• [math]x_i,\ y_i[/math]: 既知の確定値
• [math]\beta_0,\ \beta_1[/math]: 未知の確定値
• [math]Y_i,\ \varepsilon_i[/math]: 確率変数

になります。

このモデルの重要なポイントは説明変数[math]x_i[/math]を確率変数ではなく確定値としているところです。これから紹介する性質は説明変数が確率変数の場合には一般には成立しません。説明変数を実験者がコントロールできる場合は妥当な仮定ですが

• 説明変数、目的変数ともに他の変数を介して関連する場合
• 結果から要因を解析する場合

などはこの仮定が成立しなくなるので注意が必要です。

最小二乗推定量

学習データ[math]y_i[/math]を直線[math]\hat{y} = \hat{\beta}_0+\hat{\beta}_1 x[/math]で当てはめた時と同様に回帰係数[math]\beta_0,\ \beta_1[/math]の推定量を

[math]
\begin{eqnarray}
\hat{\beta}_1 &=& \dfrac{1}{S_{xx}}\sum_{i=1}^N (x_i – \bar{x})(Y_i – \bar{Y}) \\
\hat{\beta}_0 &=& \bar{Y} – \hat{\beta}_1\bar{x}
\end{eqnarray}
[/math]

で定義し最小二乗推定量やOLS（Ordinal Least Square）推定量と呼びます。ここで

• [math]\bar{x}=\frac{1}{N}\sum_{i=1}^N x_i[/math]: 確定値
• [math]\bar{Y}=\frac{1}{N}\sum_{i=1}^N Y_i[/math]: 確率変数
• [math]S_{xx}=\sum_{i=1}^N (x_i-\bar{x})^2[/math]: 確定値

です。

線形性

[math]\hat{\beta}_1[/math]は

[math]
\begin{eqnarray}

\hat{\beta}_1 &=& \dfrac{1}{S_{xx}}\sum_{i=1}^N (x_i – \bar{x})(Y_i – \bar{Y}) \\
&=& \dfrac{1}{S_{xx}}\left\{\sum_{i=1}^N (x_i – \bar{x})Y_i – \bar{Y}\sum_{i=1}^N (x_i – \bar{x}) \right\} \\
&=& \sum_{i=1}^N \dfrac{x_i – \bar{x}}{S_{xx}}Y_i
\end{eqnarray}
[/math]

とかけ[math]x_i,\ \bar{x},\ S_{xx}[/math]は確定値なので[math]\hat{\beta}_1[/math]は[math]Y_i[/math]の線形推定量です。同様に[math]\hat{\beta}_0[/math]も線形推定量です。

不偏性

最小二乗推定量[math]\hat{\beta}_0,\ \hat{\beta}_1[/math]は不偏性を持っていることを確認しましょう。

まず[math]E[Y_i]=\beta_0 + \beta_1 x_i[/math], [math]E[\bar{Y}]=\beta_0 + \beta_1 \bar{x}[/math]なので

[math]
\begin{eqnarray}
E[\hat{\beta}_1] &=& \dfrac{1}{S_{xx}}\sum_{i=1}^N (x_i – \bar{x})(E[Y_i] – E[\bar{Y}]) \\
&=& \dfrac{\beta_1}{S_{xx}}\sum_{i=1}^N (x_i – \bar{x})^2 \\
&=& \beta_1
\end{eqnarray}
[/math]

が成立し

[math]
\begin{eqnarray}
E[\hat{\beta}_0] &=& E[\bar{Y}] – E[\hat{\beta}_1]\bar{x} \\
&=& \beta_0 + \beta_1 \bar{x} – \beta_1 \bar{x} \\
&=& \beta_0
\end{eqnarray}
[/math]

が成立します。これより[math]\hat{\beta}_0,\ \hat{\beta}_1[/math]はそれぞれ[math]\beta_0,\ \beta_1[/math]の不偏推定量です。

ガウス・マルコフの定理

最小二乗推定量[math]\hat{\beta}_1[/math]は最良線形不偏推定量になることが知られており「ガウス・マルコフの定理」と呼ばれます。

[math]\tilde{\beta}_1[/math]を任意の線形推定量とすると[math]\boldsymbol{c}=(c_1,c_2,\dots,c_N)^T\in \mathbb{R}^N[/math]を用いて

[math]
\tilde{\beta}_1 = \sum_{i=1}^N c_i Y_i
[/math]

とかけます。[math]\tilde{\beta}_1[/math]が不偏推定量になるための[math]\boldsymbol{c}[/math]の条件を求めると

[math]
\begin{eqnarray}
E[\tilde{\beta}_1] &=& \beta_0\sum_{i=1}^N c_i + \beta_1 \sum_{i=1}^N c_ix_i \\
&=& \beta_1
\end{eqnarray}
[/math]

が恒等的に成立するので[math]\boldsymbol{e}=(1, 1, \dots, 1)^T, \boldsymbol{x}=(x_1, x_2, \dots, x_N)^T\in \mathbb{R}^N[/math]とおくと

[math]
\begin{eqnarray}
\boldsymbol{c}^T \boldsymbol{e} &=& 0 \\
\boldsymbol{c}^T \boldsymbol{x} &=& 1
\end{eqnarray}
[/math]

になります。これを図示すると下図の赤線部が不偏推定量になる領域です。

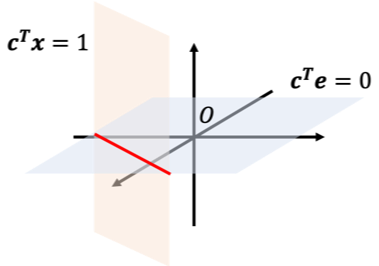
ここで[math]\tilde{\beta}_1[/math]の分散を求めると[math]V[Y_i]=\sigma^2[/math]および[math]\varepsilon_i[/math]が無相関なので

[math]
\begin{eqnarray}


V\left[\tilde{\beta}_1\right] &=& V\left[\sum_{i=1}^N c_i Y_i\right] \\
&=& \sum_{i=1}^N c_i^2 V[Y_i] \\
&=& \sigma^2\sum_{i=1}^Nc_i^2 \\
&=& \sigma^2 \|\boldsymbol{c}\|^2
\end{eqnarray}
[/math]

とかけます。

[math]\hat{\beta}_1=\sum_{i=1}^{N} \frac{x_i-\bar{x}}{S_{xx}}Y_i[/math]なので[math]\boldsymbol{b}=\frac{1}{S_{xx}}\left(x_1-\bar{x}, x_2-\bar{x},\dots, x_N-\bar{x}\right)\in\mathbb{R}^N[/math]とおくと

[math]

V\left[\hat{\beta}_1\right] = \sigma^2 \|\boldsymbol{b}\|^2
[/math]

とかけます。

[math]\hat{\beta}_1, \tilde{\beta}_1[/math]の関係は下図になり[math]\|\boldsymbol{b}\|^2, \|\boldsymbol{c}\|^2[/math]の大小関係から分散[math]V[\hat{\beta}_1], V[\tilde{\beta}_1][/math]を評価します。

[math]\overrightarrow{O\hat{\beta}_1}[/math]と[math]\overrightarrow{\hat{\beta}_1\tilde{\beta}_1}[/math]の内積を計算すると[math]\|\boldsymbol{b}\|^2 = \frac{1}{S_{xx}}[/math]および[math]\boldsymbol{b}=\frac{\boldsymbol{x}-\bar{x}\boldsymbol{e}}{S_{xx}}[/math]とかけるので

[math]
\begin{eqnarray}
&& 
\boldsymbol{b}^T (\boldsymbol{c} – \boldsymbol{b}) \\
&=& \boldsymbol{c}^T\boldsymbol{b} – \|\boldsymbol{b}\|^2 \\
&=& \dfrac{1}{S_{xx}}(\boldsymbol{c}^T\boldsymbol{x} – \bar{x}\boldsymbol{c}^T\boldsymbol{e}) – \|\boldsymbol{b}\|^2 \\
&=& \dfrac{1}{S_{xx}} – \dfrac{1}{S_{xx}} \\
&=& 0
\end{eqnarray}
[/math]

より直交することがわかります。これより

[math]
\begin{eqnarray}

\|\boldsymbol{c}\|^2 &=& \|\boldsymbol{b} + (\boldsymbol{c}-\boldsymbol{b}) \|^2 \\
&=& 
\|\boldsymbol{b}\|^2 + 
\|\boldsymbol{c}-\boldsymbol{b}\|^2 \\
&\geq & \|\boldsymbol{b}\|^2
\end{eqnarray}
[/math]

が成立するので

[math]
\begin{eqnarray}



V\left[\tilde{\beta}_1\right] &=& \sigma^2 \|\boldsymbol{c}\|^2 \\
&\geq &\sigma^2 \|\boldsymbol{b}\|^2 \\
&=& 


V\left[\hat{\beta}_1\right]
\end{eqnarray}
[/math]

が成立し、最小二乗推定量[math]\hat{\beta}_1[/math]は最良線形不偏推定量になることがわかります。

シリーズ記事

「機械学習」の「教師あり学習手法」の中で最も基本的な手法として「単回帰」の性質を紹介しています。

ここでは誤差項が「無相関で分散一定」を仮定すると

最小二乗推定量は最良線形不偏推定量になる

ことを示しました。「最尤推定量」以降の記事では誤差項が「独立同一な正規分布」を仮定し様々な性質を導いていきます。

また単回帰を拡張した「重回帰」でも同様の性質を示せるのでそちらも参照ください。