コメント
大問3は品質管理で使われる「工程能力指数」をテーマにした問題が出題されました。他の大問と比べ量/難度が高く時間内での完答は厳しい問題セットです。
問1は簡単な問題であることが多いのですが、この大問の問1は一見当たり前の事実ですが、きちんと示そうとすると少し骨が折れます。
問2~4は難しくないですが問題量が多くここで時間切れになった人も多いと思います。
最後の問5は[math]C_P[/math]とカイ二乗分布が出てくる形に変形するところが第一関門で、その後も「解法1. 定義に基づいて計算」で紹介した「確率密度関数の定義域上での積分に帰着させる」などの工夫をしても計算が大変で完答できた人は少なかったでしょう。
問題
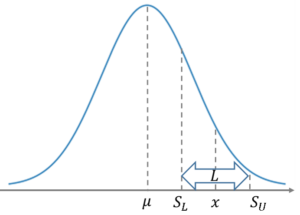
- 下側規格:[math]S_L[/math]
- 上側規格:[math]S_U[/math]
とし区間[math](S_L, S_U)[/math]を外れた場合は不良品とする。工程能力指数[math]C_p[/math]を
- 母標準偏差[math]\sigma[/math]が既知:[math]C_p=\dfrac{S_U-S_L}{6\sigma}[/math]
- 母標準偏差[math]\sigma[/math]が未知:[math]\hat{C}_p=\dfrac{S_U-S_L}{6S}[/math]
とする。ここで、[math]X_1,\dots,X_n[/math]を無作為標本とし
- 標本平均:[math]\bar{X}=\dfrac{1}{n}\sum_{i=1}^nX_i[/math]
- 標本標準偏差:[math]S=\sqrt{\dfrac{1}{n-1}\sum_{i=1}^n(X_i-\bar{X})^2}[/math]
とする時、以下の問に答えよ。
(出典:2016年受験時の問題冊子。問題文を一部略記。)
問1
適合品率(=1-不良率)が[math]\mu=\frac{S_L+S_U}{2}[/math]の時に最大になることを示す。
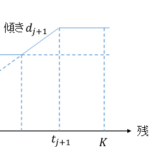
上側/下側規格の幅を[math]L(=S_U-S_L)[/math]としその中点を[math]x=\frac{S_L+S_U}{2}[/math]とすると適合品率[math]G(x)[/math]は正規分布の累積分布関数を[math]\Phi(x)[/math]を用いて
[math]
G(x) = \Phi\left(x+\frac{L}{2}\right) – \Phi\left(x-\frac{L}{2}\right)
[/math]
とかけ、正規分布の確率密度関数を[math]f(x)[/math]とすると
[math]
G'(x) = f\left(x+\frac{L}{2}\right) – f\left(x-\frac{L}{2}\right)
[/math]
となる。ここで、[math]f(x)[/math]の単調性と対称性に注意して増減表を求めると
[math]
\begin{array}{|c|*3{c|}}\hline
x & \cdots & \mu & \cdots \\ \hline
G'(x) & + & 0 & – \\ \hline
G(x) & \nearrow & G(\mu) & \searrow \\ \hline
\end{array}
[/math]
となる。これより[math]x=\mu[/math]、つまり[math]\mu=\frac{S_L+S_U}{2}[/math]の時、適合品率[math]G(x)[/math]は最大値を取る。
問2
[math]C_P=\frac{2}{3}[/math]より[math]S_U-S_L=4\sigma[/math]である。これより不良率[math]F[/math]は区間[math][\mu-2\sigma, \mu+2\sigma][/math]の外の区間の確率、つまり標準正規分布において区間[math][-2, 2][/math]の外の区間の確率なので
[math]
F = 2Q(2)=0.0456
[/math]
である。([math]Q(u)[/math]は標準正規分布の上側確率を表す。)
問3
[math]I_C=\left(\hat{C}_P\sqrt{\dfrac{\chi^2_{0.975}(n-1)}{n-1}},\ \hat{C}_P\sqrt{\dfrac{\chi^2_{0.025}(n-1)}{n-1}}\right)[/math]
となることを示せ。なお[math]\chi^2_\alpha(\nu)[/math]は自由度[math]\nu[/math]のカイ二乗分布の上側[math]100\alpha\%[/math]点である。
[math]
\begin{eqnarray}
Y&=&(n-1)C_P^2 / \hat{C}_P^2 \\
&=&\sum_{i=1}^n(X_i-\bar{X})^2/\sigma^2 \\
&\sim& \chi^2(n-1)
\end{eqnarray}
[/math]
より
[math]
\begin{eqnarray}
&&P\left(\chi^2_{0.975}(n-1)\leq Y \leq \chi^2_{0.025}(n-1) \right) \\
&=& 0.95
\end{eqnarray}
[/math]
が成立し、式変形することで
[math]P\left(C_P\in I_C\right)=0.95[/math]
が得られる。
問4
- [math]\hat{C}_P[/math]を求めよ。
- [math]C_P[/math]の信頼係数[math]95\%[/math]の信頼区間を求めよ。
- [math]C_P\geq 1.33[/math]が望ましいとした時、この工程の管理状態を解釈せよ。
まず[math]\hat{C}_P=\frac{12.6-12.0}{6\times 0.05}=2[/math]である。
[math]C_P[/math]の信頼係数[math]95\%[/math]の信頼区間は問3の結果および[math]\chi^2_{0.975}(19)=8.91, \chi^2_{0.025}(19)=32.85[/math]から[math][1.37,\ 2.63][/math]である。
[math]C_P[/math]の点推定値は[math]2[/math]であり信頼区間の下限も[math]1.37[/math]と[math]1.33[/math]より大きいためこの工程は十分な管理状態であると言える。
問5
[math]f(y)=\dfrac{1}{2\Gamma(\nu/2)}\left(\dfrac{y}{2}\right)^{\nu/2-1}e^{-y/2}[/math]
であることは既知として良い。
まず
[math]
\begin{eqnarray}
E\left[\hat{C}_P\right]&=&E\left[\dfrac{S_U-S_L}{6S}\right] \\
&=& \dfrac{S_U-S_L}{6\sigma}E\left[\dfrac{\sigma}{S}\right] \\
&=& C_P\sqrt{n-1} \cdot E\left[\dfrac{\sigma}{S\sqrt{n-1}}\right]
\end{eqnarray}
[/math]
より、[math]Y[/math]を自由度[math]n-1[/math]のカイ二乗分布に従う確率変数とすると
[math]
E\left[\hat{C}_P\right] = C_P\sqrt{n-1} \cdot E\left[Y^{-1/2}\right]
[/math]
とかける。
ここで[math]\nu=n-1[/math]と置いて[math]E\left[Y^{-1/2}\right][/math]を求めると
[math]
\begin{eqnarray}
&&E\left[Y^{-1/2}\right] \\
&=& \int_0^{\infty}y^{-1/2}f(y)dy \\
&=& \dfrac{1}{2\Gamma(\nu / 2)}\int_0^{\infty}y^{-1/2}\left(\dfrac{y}{2}\right)^{\nu/2 – 1}e^{-y/2} dy \\
&=& \dfrac{\Gamma\left((\nu-1) / 2\right)}{\sqrt{2}\Gamma(\nu / 2)}\\
&&\ \cdot \dfrac{1}{2\Gamma\left((\nu-1) / 2\right)} \int_0^{\infty}\left(\dfrac{y}{2}\right)^{\frac{\nu-1}
{2} – 1}e^{-y/2} dy
\end{eqnarray}
[/math]
となり第二項は[math]\chi^2(\nu-1)[/math]分布の定義域全体での積分なので[math]1[/math]になり
[math]
\begin{eqnarray}
E\left[Y^{-1/2}\right] = \dfrac{\Gamma\left((n-2) / 2\right)}{\sqrt{2}\Gamma\left((n-1) / 2\right)}
\end{eqnarray}
[/math]
となる。以上より
[math]E[\hat{C}_P] / C_P=\sqrt{\dfrac{n-1}{2}} \cdot \dfrac{\Gamma\left((n-2) / 2\right)}{\Gamma\left((n-1) / 2\right)}[/math]
である。
シリーズ記事
- 過去問と解答例
- 2016年(理工学)大問1
- 2016年(理工学)大問1 解答例
- 2016年(理工学)大問3
- 2016年(理工学)大問3 解答例(本記事)
- 2016年(理工学)大問4
- 2016年(理工学)大問4 解答例