コメント
大問1はガンマ分布に関する問題が出題されました。問4までは特に悩むことなく進められると思いますが、問5で問題文中の「[math]\eta(\alpha)[/math]が単調増加関数であることを用いてよい。」という文言を「狭義単調増加」と捉えてよいのかで難度に天と地の差が出ます。
ここでは[math]\eta(\alpha)[/math]が狭義単調増加であることも示しますが試験会場で思いつくのは限りなく不可能な解答だと思います。正直、簡単に示す方法が分からなかったので公式問題集の解答が出たら修正したいと思います。
問題
[math]
f(x)=\begin{cases}\dfrac{1}{\beta^\alpha \Gamma(\alpha)}x^{\alpha-1}e^{-x/\beta} &(x > 0) \\ 0 &(x \leq 0)\end{cases}
[/math]
である。[math]n[/math]個の電子部品の寿命の試験結果[math]X_1,\dots,X_n[/math]の実現値を[math]x_1,\dots,x_n[/math]とし[math]x_1=\cdots=x_n[/math]ではないとする。この時、以下の問に答えよ。
(出典:統計検定HP「統計検定 1級の過去問題」。問題文を一部略記。)
問1
まず期待値を求めると[math]\Gamma(\alpha+1)=\alpha\Gamma(\alpha)[/math]に注意して
[math]
\begin{eqnarray}
&& E[X] \\
&=& \int_{0}^\infty \dfrac{1}{\beta^\alpha\Gamma(\alpha)}x^\alpha e^{-x/\beta}dx \\
&=& \alpha\beta\int_{0}^\infty \dfrac{1}{\beta^{\alpha+1}\Gamma(\alpha+1)}x^\alpha e^{-x/\beta}dx \\
\end{eqnarray}
[/math]
であり積分部分は[math]Gamma(\alpha+1,\beta)[/math]の定義域全体での積分なので[math]1[/math]になり、これより[math]E[X]=\alpha\beta[/math]である。
同様に[math]E[X^2][/math]を求めると[math]E[X^2]=\alpha(\alpha+1)\beta^2[/math]を得るので
[math]
\begin{eqnarray}
V[X] &=& E[X^2] – (E[X])^2 \\
&=& \alpha(\alpha+1)\beta^2 – \alpha^2\beta^2\\
&=& \alpha\beta^2
\end{eqnarray}
[/math]
を得る。
問2
対数尤度関数を求めると
[math]
\begin{eqnarray}
&& l(\alpha, \beta;\ \mathbf{x}) \\
&=& \sum_{i=1}^n \log f(x_i) \\
&=& -n\alpha \log\beta -n\log\Gamma(\alpha) \\
&& + (\alpha – 1)\sum_{i=1}^n\log x_i – \dfrac{1}{\beta}\sum_{i=1}^n x_i
\end{eqnarray}
[/math]
である。
問3
[math]\bar{x}_n, \tilde{x}_n[/math]を用いると対数尤度関数は
[math]
\begin{eqnarray}
&& l(\alpha, \beta;\ \mathbf{x}) \\
&=& -n\left\{\alpha \log\beta +\log\Gamma(\alpha)\right. \\
&& \quad \left. – (\alpha – 1)\log \tilde{x}_n + \bar{x} / \beta \right\}
\end{eqnarray}
[/math]
とかける。[math]\alpha, \beta[/math]でそれぞれ偏微分して尤度方程式を求めると
[math]
\begin{cases}
-n(\log\beta+\psi(\alpha)-\log\tilde{x}_n)=0 \\
-n\left(\dfrac{\alpha}{\beta} – \dfrac{\bar{x}_n}{\beta^2} \right) = 0
\end{cases}
[/math]
になり、これを解いて
[math]
\begin{cases}
\psi(\alpha)-\log\alpha=\log\dfrac{\tilde{x}_n}{\bar{x}_n} \\
\beta=\dfrac{\bar{x}_n}{\alpha}
\end{cases}
[/math]
を得る。
問4
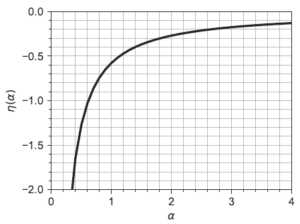
[math]\bar{x}_n=1000[/math], [math]\log\tilde{x}_n=6.36[/math]より[math]\eta(\alpha)=-0.547[/math]でありグラフより[math]\alpha=1[/math]である。これより[math]\beta=\frac{\bar{x}_n}{\alpha}=1000[/math]である。
問5
簡単な解法が思いつかなかったので、ここでは[math]\dfrac{d}{d\alpha}\psi(a)=\displaystyle\sum_{n=0}^\infty\dfrac{1}{(\alpha + n)^2}[/math]と級数表示できる(参考:Wikipedia「ディガンマ関数」)ことを使って示します。
[math]\eta'(\alpha)=\psi'(a)-1/\alpha[/math]であり[math]\psi'(a)[/math]は
[math]
\psi'(a)=\displaystyle\sum_{n=0}^\infty\dfrac{1}{(\alpha + n)^2}
[/math]
と書けることに注意する。
ここで関数[math]y=1/x^2[/math]の区間[math][\alpha+n,\ \alpha+n+1][/math]の面積と高さ[math]1/(\alpha+n)^2[/math]、幅[math]1[/math]の矩形の面積を比較すると
[math]
\dfrac{1}{(\alpha+n)^2} > \displaystyle\int_{\alpha+n}^{\alpha+n+1} \dfrac{1}{x^2}dx
[/math]
が成立する。[math]n=0,1,2,\dots[/math]について両辺の和をとって
[math]
\begin{eqnarray}
\sum_{n=0}^\infty\dfrac{1}{(\alpha + n)^2} &>& \displaystyle\int_{\alpha}^{\infty} \dfrac{1}{x^2}dx \\
&=& \dfrac{1}{\alpha}
\end{eqnarray}
[/math]
を得る。これより任意の[math]\alpha > 0[/math]で
[math]
\eta'(\alpha) > 0
[/math]
なので[math]\eta(\alpha)[/math]は[math]\alpha > 0[/math]で狭義に単調増加である。
したがって[math]\eta(\alpha)[/math]は[math]\eta(\alpha)=\log\dfrac{\tilde{x}_n}{\bar{x}_n}[/math]は[math]\alpha[/math]について一意の解を持ち、この[math]\alpha[/math]から[math]\beta[/math]も一意にきまるので[math]\alpha, \beta[/math]の最尤推定値は一意に存在する。
シリーズ記事
- 過去問と解答例
- 2017年(理工学)大問1
- 2017年(理工学)大問1 解答例(本記事)
- 2017年(理工学)大問2
- 2017年(理工学)大問2 解答例
- 2017年(理工学)大問3
- 2017年(理工学)大問3 解答例