単回帰モデル構築時の外れ値の影響

単回帰は学習データに外れ値があると

外れ値への当てはまりを優先し他のデータの当てはまりをほぼ無視する

ことが知られています。ここでは実例を通して外れ値がどのような影響を与えるかを確認しで外れ値が与える影響を理論的に解析します。

なお、PythonスクリプトをGitHub上にあげているのでそちらも参照ください。

外れ値の影響例

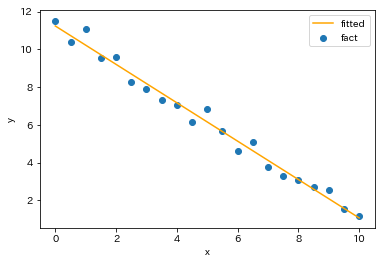
まず実例を通して外れ値の影響をみてみましょう。外れ値を含まないデータとして

で単回帰モデルを構築すると以下が得られます。

うまく当てはまっていますし決定係数も[math]0.984[/math]と高い値になっています。

次にこの学習データに点[math](100,\ 100)[/math]を追加してみます。

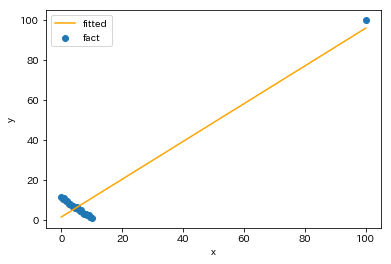
このデータで単回帰モデルを構築すると

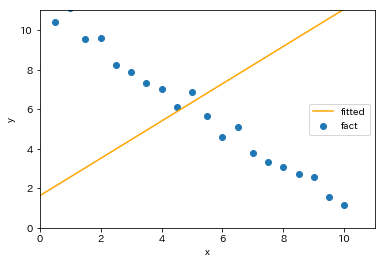
と外れ値付近と元の学習データの重心付近を通る回帰直線が得られます。たった1点追加しただけで先ほどとは大きく異なる結果になります。元の学習データ付近を拡大すると

と外れ値以外の学習データでは全く当てはまっていないことがわかります。実際、外れ値が存在する場合

外れ値への当てはまりを優先し他のデータの当てはまりをほぼ無視する

ことが知られています。そのため単回帰でモデルを作る際には

• 説明変数に外れ値がないか確認
• 外れ値がある場合は正常値か否か、つまりモデルで表現したい値かを確認
  • 正常値の場合は丸め処理、ビン分割、対数変換や非線形モデルを検討
  • 異常値の場合はデータ除去を検討

することをオススメします。

なおこのモデルの決定係数は[math]0.912[/math]と高い値^[1]点[math](100,\ 100)[/math]ではなく点[math](1000,\ 1000)[/math]を追加すると決定係数は[math]0.999[/math]まで上がります。になります。このことからも決定係数の数字だけでモデルの良し悪しを判断せず可視化して確認する必要があります。

外れ値の影響解析

ここでは外れ値が回帰直線がどう影響を与えるかを見ます。具体的には

• 学習データ: [math](x_i, y_i),\ i=1,2,\dots,N[/math]

に

• 外れ値: 点[math](x_{N+1}, y_{N+1})[/math]

が加わったときに回帰直線がどう変化するかを解析します。

簡単のために元の学習データの重心が原点となるように座標系を取ります。つまり、[math]\sum_{i=1}^N x_i = \sum_{i=1}^N y_i = 0[/math]とします。元の学習データでの単回帰モデル[math]

y = 
\hat{\beta}_{N,0} + 
\hat{\beta}_{N,1} x[/math]は

[math]
\begin{eqnarray}

\hat{\beta}_{N,0} &=& 0 \\

\hat{\beta}_{N,1} &=& \dfrac{S_{x_Ny_N}}{S_{x_Nx_N}}
\end{eqnarray}
[/math]

で与えられます。ここで[math]S_{x_Ny_N} = \sum_{i=1}^N x_iy_i[/math], [math]S_{x_Nx_N} = \sum_{i=1}^N x_i^2[/math]です。

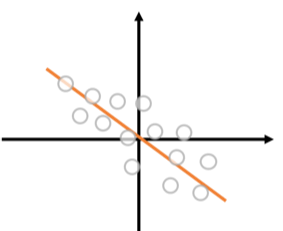
ここで学習データに外れ値[math](x_{N+1}, y_{N+1})[/math]を加えます。

この時、以下の命題が成立します。

つまり外れ値を追加後の回帰直線は外れ値と原点を通る直線に近い直線になり、元の学習データにほとんど関係ない直線が得られることがわかります。

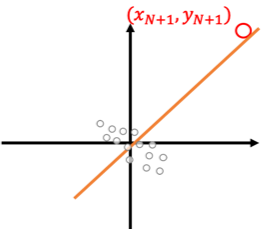
ここからは命題を以下のステップで示します。

1. データ追加後の回帰係数[math]\hat{\beta}_{N+1,0},\ \hat{\beta}_{N+1,1}[/math]の算出
2. [math]S_{x_{N+1}y_{N+1}}[/math]と[math]S_{x_{N}y_{N}}[/math]の関係
3. [math]S_{x_{N+1}x_{N+1}}[/math]と[math]S_{x_{N}x_{N}}[/math]の関係
4. 回帰係数[math]\hat{\beta}_{N+1,0},\ \hat{\beta}_{N+1,1}[/math]の近似評価

データ追加後の回帰係数[math]\hat{\beta}_{N+1,0},\ \hat{\beta}_{N+1,1}[/math]の算出

まず追加後の学習データの平均は

[math]
\begin{eqnarray}

\bar{x}_{N+1} &=& \dfrac{x_{N+1}}{N+1} \\

\bar{y}_{N+1} &=& \dfrac{y_{N+1}}{N+1}
\end{eqnarray}
[/math]

になります。また、単回帰モデル[math]

y = 
\hat{\beta}_{N+1,0} + 
\hat{\beta}_{N+1,1} x[/math]は

[math]
\begin{eqnarray}

\hat{\beta}_{N+1,0} &=& 
\bar{y}_{N+1} – 
\hat{\beta}_{N+1,1}
\bar{x}_{N+1} \\

\hat{\beta}_{N+1,1} &=& \dfrac{S_{x_{N+1}y_{N+1}}}{S_{x_{N+1}x_{N+1}}}
\end{eqnarray}
[/math]

で与えられます。ここで

[math]
\begin{eqnarray}
S_{x_{N+1}y_{N+1}} &=& \sum_{i=1}^{N+1} (x_i – 
\bar{x}_{N+1})(y_i – 
\bar{y}_{N+1}) \\
S_{x_{N+1}x_{N+1}} &=& \sum_{i=1}^{N+1} (x_i – 
\bar{x}_{N+1})^2
\end{eqnarray}
[/math]

です。

[math]S_{x_{N+1}y_{N+1}}[/math]と[math]S_{x_{N}y_{N}}[/math]の関係

点[math](x_{N+1},\ y_{N+1})[/math]の影響を見るために[math]S_{x_{N+1}y_{N+1}}[/math]を[math]S_{x_{N}y_{N}}[/math]で表現することを考えます。

[math]
\begin{eqnarray}

&& S_{x_{N+1}y_{N+1}} \\
&=& \sum_{i=1}^{N+1} (x_i – 
\bar{x}_{N+1})(y_i – 
\bar{y}_{N+1}) \\
&=& \sum_{i=1}^{N} (x_i – 
\bar{x}_{N+1})(y_i – 
\bar{y}_{N+1}) \\
&&\quad + (x_{N+1} – 
\bar{x}_{N+1})(y_{N+1} – 
\bar{y}_{N+1})
\end{eqnarray}
[/math]

であり第一項は[math]\sum_{i=1}^N x_i = \sum_{i=1}^N y_i = 0[/math]より

[math]
\begin{eqnarray}

&& \sum_{i=1}^{N} (x_i – 
\bar{x}_{N+1})(y_i – 
\bar{y}_{N+1}) \\
&=& \sum_{i=1}^{N}\left(x_iy_i – x_i\bar{y}_{N+1} -y_i\bar{x}_{N+1}+\bar{x}_{N+1}\bar{y}_{N+1}\right) \\
&=& S_{x_{N}y_{N}} + N\bar{x}_{N+1}\bar{y}_{N+1} \\
&=& S_{x_{N}y_{N}} + \dfrac{N}{(N+1)^2}x_{N+1}y_{N+1}
\end{eqnarray}
[/math]

であり、第二項は

[math]
\begin{eqnarray}

&& (x_{N+1} – 
\bar{x}_{N+1})(y_{N+1} – 
\bar{y}_{N+1}) \\
&=& \dfrac{N^2}{(N+1)^2}x_{N+1}y_{N+1}
\end{eqnarray}
[/math]

となるので整理して

[math]

S_{x_{N+1}y_{N+1}} = S_{x_{N}y_{N}} + \dfrac{N}{N+1}x_{N+1}y_{N+1}
[/math]

が成立します。

[math]S_{x_{N+1}x_{N+1}}[/math]と[math]S_{x_{N}x_{N}}[/math]の関係

同様に[math]S_{x_{N+1}x_{N+1}}[/math]を[math]S_{x_{N}x_{N}}[/math]使って表現します。

[math]
\begin{eqnarray}
&& S_{x_{N+1}x_{N+1}} \\
&=& \sum_{i=1}^{N+1} (x_i – \bar{x}_{N+1})^2 \\
&=& \sum_{i=1}^{N} (x_i^2 – 2\bar{x}_{N+1}x_i + \bar{x}_{N+1}^2) + (x_{N+1} – \bar{x}_{N+1})^2 \\
&=& S_{x_{N}x_{N}} + N\bar{x}_{N+1}^2 + \dfrac{N^2}{(N+1)^2}x_{N+1}^2 \\
&=& S_{x_{N}x_{N}} + \dfrac{N}{N+1}x_{N+1}^2
\end{eqnarray}
[/math]

が得られます。

回帰係数[math]\hat{\beta}_{N+1,0},\ \hat{\beta}_{N+1,1}[/math]の近似評価

これよりデータ追加後の回帰曲線の傾きは

[math]
\begin{eqnarray}
\hat{\beta}_{N+1,1} &=& \dfrac{S_{x_{N+1}y_{N+1}}}{S_{x_{N+1}x_{N+1}}} \\
&=& \dfrac{S_{x_{N}y_{N}} + \frac{N}{N+1}x_{N+1}y_{N+1}}{S_{x_{N}x_{N}} + \frac{N}{N+1}x_{N+1}^2 }
\end{eqnarray}
[/math]

となります。ここで[math]x_{N+1}^2 \gg S_{x_{N}x_{N}}[/math]および[math]x_{N+1}y_{N+1} \gg S_{x_{N}y_{N}}[/math]のとき

[math]
\begin{eqnarray}
\hat{\beta}_{N+1,1} \approx \dfrac{y_{N+1}}{x_{N+1}}
\end{eqnarray}
[/math]

になり回帰係数の切片は

[math]
\begin{eqnarray}
\hat{\beta}_{N+1,0} &=& 
\bar{y}_{N+1} – 
\hat{\beta}_{N+1,1}
\bar{x}_{N+1} \\
&\approx & \dfrac{y_{N+1}}{N+1} – \dfrac{y_{N+1}}{x_{N+1}}\dfrac{x_{N+1}}{N+1} \\
&=& 0
\end{eqnarray}
[/math]

になります。

以上より外れ値[math](x_{N+1}, y_{N+1})[/math]が十分大きく[math]x_{N+1}^2 \gg S_{x_{N}x_{N}}[/math]および[math]x_{N+1}y_{N+1} \gg S_{x_{N}y_{N}}[/math]が成立するとき、回帰曲線は近似的に原点と点[math](x_{N+1},\ y_{N+1})[/math]を通る直線で与えられます。

シリーズ記事

「機械学習」の「教師あり学習手法」の中で最も基本的な手法として「単回帰」の性質を紹介しています。

誤差項について「無相関で分散一定」「独立同一な正規分布」を仮定するとで様々な性質を導くことができますが、ここでは誤差項について特に仮定せずに導ける性質として

• 考え方と基本的な性質: 回帰係数の導出、回帰直線の性質、計算量との関係
• 決定係数: 決定係数と相関係数の関係
• 予測の留意点: 学習データ外の値や外れ値で予測する場合の留意点と対処法
• 外れ値の影響（本記事）: 外れ値が学習時に与える影響

を解説しています。

また単回帰を拡張した「重回帰」でも同様の性質を示せるのでそちらも参照ください。