重回帰の考え方と基本的な性質

投稿者: | 2019-08-11
0件のコメント

単回帰では説明変数が1つでしたが、説明変数を複数に拡張したモデルが重回帰（multiple linear regression）です。ここでは重回帰の考え方と基本的な性質として

  • 回帰係数の導出
  • 回帰超平面の性質
  • 計算量

を紹介します。行列やベクトル演算が多く何をしているか理解しづらいと感じた方は

も合わせて参照ください。

重回帰

重回帰は[math]P[/math]個の説明変数[math]x_{1},\ x_{2},\dots,\ x_{P}[/math]と目的変数[math]y[/math]の間の関係

[math]

y = \beta_0 + \beta_1 x_1 + \cdots + \beta_P x_P,\ \beta_0, \dots, \beta_P \in \mathbb{R}
[/math]

を[math]N[/math]個の学習データ、つまり入出力データの組

  • 入力データ: [math](x_{i,1},\ x_{i,2},\dots,\ x_{i,P}) \in \mathbb{R}^P[/math]
  • 出力データ: [math]y_i\in \mathbb{R}[/math]

から求める手法です[math](i=1,2,\dots,N)[/math]。超平面[math]y=\beta_0 + \beta_1 x_1 + \cdots + \beta_P x_P[/math]を回帰超平面と呼び、[math]\beta_0, \beta_1, \dots, \beta_P[/math]を偏回帰係数や回帰係数と呼びます。説明変数[math]x_p[/math]が1単位を大きくなると目的変数[math]y[/math]が[math]\beta_i[/math]だけ大きくなることを表しており解釈しやすいモデルです。

単回帰と同様にデータさえあれば回帰直線を求めることができますが、重回帰は

  • 目的変数と説明変数間に比例関係を仮定
  • 各説明変数が目的変数に与える影響は独立と仮定

しており学習データで本当に仮定が成立しているか確認しておく必要があります。

損失関数

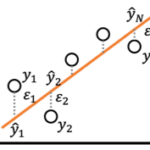
回帰係数[math](\beta_0,\dots,\beta_P)[/math]を動かすと回帰超平面を動かすことができます。回帰超平面の良し悪しを予測値[math]\hat{y}_i=\beta_0 + \sum_p \beta_p x_{i,p}[/math]と目的変数[math]y_i[/math]の差[math]

\varepsilon_i= y_i – \hat{y}_i[/math]の二乗和

[math]
\begin{eqnarray}
&& 
L(\beta_0, \dots, \beta_P) \\
&=& \sum_{i=1}^N \varepsilon_i^2 \\
&=& \sum_{i=1}^N \left( y_i – \left(\beta_0 + \sum_p \beta_p x_{i,p}\right) \right)^2
\end{eqnarray}
[/math]

で表現し、[math]
L(\beta_0, \dots, \beta_P)[/math]を最小化する[math](\beta_0, \dots, \beta_P)[/math]を求めます。モデルのパラメタを決定するために用いる関数[math]L[/math]を損失関数（Loss function）と呼びます。

ベクトル、行列表記

重回帰の性質はベクトル、行列で表記することで見通しよく議論できます。ここでは

  • 説明変数: [math]\boldsymbol{x}=(1,x_1,\dots,x_P)^T\in \mathbb{R}^{P+1}[/math]
  • 回帰係数: [math]\boldsymbol{\beta}=(\beta_0,\beta_1,\dots,\beta_P)^T\in \mathbb{R}^{P+1}[/math]
  • 学習データ
    • 出力データ: [math]\boldsymbol{y}=(y_1,\dots,y_N)^T\in\mathbb{R}^N[/math]
    • 入力データ:
      [math]
      \begin{eqnarray}
      
\boldsymbol{e} &=& (1,\ 1,\dots,\ 1)^T\in\mathbb{R}^N \\
      \boldsymbol{x}_i &=& (x_{1,i},\ x_{2,i},\dots,\ x_{N,i})^T\in\mathbb{R}^N \\
      \boldsymbol{X} &=& \left(
\boldsymbol{e}\ 
\boldsymbol{x}_1 \cdots \boldsymbol{x}_P \right)\in \mathbb{R}^{N \times (P+1)}
      \end{eqnarray}
      [/math]

と表記します。この時、回帰超平面は

[math]

y = \boldsymbol{\beta}^T \boldsymbol{x}
[/math]

とかけます。また、[math]i[/math]番目の入力データの予測値は

[math]

\hat{y}_i = \boldsymbol{X}_i\boldsymbol{\beta}
[/math]

とかけます。ここで[math]\boldsymbol{X}_i[/math]は行列[math]\boldsymbol{X}[/math]の第[math]i[/math]行目を表します。

また損失関数[math]L(\boldsymbol{\beta})[/math]は

[math]
\begin{eqnarray}

L(\boldsymbol{\beta}) &=& \sum_{i=1}^N (y_i – \hat{y}_i)^2 \\
&=& \left(\boldsymbol{y}-\boldsymbol{\hat{y}}\right)^T\left(\boldsymbol{y}-\boldsymbol{\hat{y}}\right) \\
&=& \left(\boldsymbol{y} – \boldsymbol{X}\boldsymbol{\beta}\right)^T\left(\boldsymbol{y} – \boldsymbol{X}\boldsymbol{\beta}\right)
\end{eqnarray}
[/math]

とかけます。

回帰係数の導出

重回帰でも損失関数[math]
L(\boldsymbol{\beta})[/math]を最小化する回帰係数[math]\boldsymbol{\hat{\beta}}[/math]を解析的に求めることができます。

[math]N \geq P+1[/math]とし、[math]{\rm rank}\ \boldsymbol{X}=P+1[/math]とする。この時、回帰係数は以下で与えられる。

[math]

\boldsymbol{\hat{\beta}} = \left(\boldsymbol{X}^T\boldsymbol{X}\right)^{-1}\boldsymbol{X}^T\boldsymbol{y}
[/math]

[math]L(\boldsymbol{\beta})=\boldsymbol{\beta}^T\boldsymbol{X}^T\boldsymbol{X}\boldsymbol{\beta}-2\boldsymbol{y}^T\boldsymbol{X}\boldsymbol{\beta}+\boldsymbol{y}^T\boldsymbol{y}[/math]と[math]\boldsymbol{\beta}[/math]の2次形式でヘッセ行列は

[math]


\dfrac{\partial^2 L}{\partial \boldsymbol{\beta}^2}=\boldsymbol{X}^T\boldsymbol{X} \succ O
[/math]

[math]\boldsymbol{X}[/math]が列フルランクなので正定値になります。これより[math]\dfrac{\partial L}{\partial \boldsymbol{\beta}}=0[/math]の解が最小解を与えます。

[math]
\begin{eqnarray}

&& 
\dfrac{\partial L}{\partial \boldsymbol{\beta}}=0 \\
& \Leftrightarrow & \boldsymbol{X}^T\boldsymbol{X}\boldsymbol{\beta} = \boldsymbol{X}^T\boldsymbol{y}
\end{eqnarray}
[/math]

となり、この式を正規方程式と呼びます。[math]N \geq P+1,\ {\rm rank}\ \boldsymbol{X}=P+1[/math]より[math]\boldsymbol{X}^T\boldsymbol{X}[/math]の逆行列が存在し

[math]
\boldsymbol{\hat{\beta}} = \left(\boldsymbol{X}^T\boldsymbol{X}\right)^{-1}\boldsymbol{X}^T\boldsymbol{y}
[/math]

が得られます。

回帰超平面の性質

学習データの平均[math](\bar{\boldsymbol{x}},\ \bar{y})[/math]との関係

単回帰と同様に回帰超平面は学習データの平均

  • 入力データの平均: [math]\bar{\boldsymbol{x}} = \left(1,\ \frac{1}{N}\sum_{i=1}^N x_{i,1},\dots,\frac{1}{N}\sum_{i=1}^N x_{i,P} \right) [/math]
  • 出力データの平均: [math]\bar{y} = \frac{1}{N}\sum_{i=1}^Ny_i[/math]

を通ることが知られています。

回帰超平面は学習データの平均[math](\bar{\boldsymbol{x}},\ \bar{y})[/math]を必ず通る。

入出力データの平均は

[math]
\begin{eqnarray}

\bar{\boldsymbol{x}} &=& \dfrac{1}{N}\boldsymbol{X}^T\boldsymbol{e} \\
\bar{y} &=& \dfrac{1}{N}\boldsymbol{y}^T\boldsymbol{e}
\end{eqnarray}
[/math]

とかけます。これより

[math]
\begin{eqnarray}

\bar{y} – \boldsymbol{\hat{\beta}}^T
\bar{\boldsymbol{x}} &=& \dfrac{1}{N}\boldsymbol{y}^T\boldsymbol{e} – \dfrac{1}{N}\boldsymbol{\hat{\beta}}^T
\boldsymbol{X}^T\boldsymbol{e} \\
&=& \dfrac{1}{N}\left(\boldsymbol{y}-\boldsymbol{X}\boldsymbol{\beta}\right)^T\boldsymbol{e} \\
&=& \dfrac{1}{N}\boldsymbol{\varepsilon}^T\boldsymbol{e} \\
&=& \dfrac{1}{N}\sum_{i=1}^N \varepsilon_i
\end{eqnarray}
[/math]

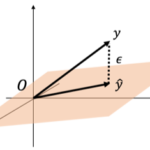
となります。ここで[math]\boldsymbol{\varepsilon}=\boldsymbol{y}-\boldsymbol{\hat{y}}[/math]です。「幾何学でみる重回帰の性質」の「残差[math]\boldsymbol{\varepsilon}[/math]の性質」でみたように残差[math]\boldsymbol{\varepsilon}[/math]の平均は0になるので

[math]


\bar{y} – \boldsymbol{\hat{\beta}}^T
\bar{\boldsymbol{x}} = 0
[/math]

が成立し回帰超平面は学習データの平均[math](\bar{\boldsymbol{x}},\ \bar{y})[/math]を通ることがわかります。

出力データ[math]\boldsymbol{y}[/math]と予測値[math]\boldsymbol{\hat{y}}[/math]の平均

残差[math]\boldsymbol{\varepsilon}=\boldsymbol{y}-\boldsymbol{\hat{y}}[/math]の平均が0になることから以下がわかります。

出力データ[math]\boldsymbol{y}[/math]の平均[math]\bar{y}[/math]と入力データの予測値[math]\boldsymbol{\hat{y}}[/math]の平均[math]\bar{\hat{y}}[/math]は一致する。

簡単な計算から示すことができます。

[math]
\begin{eqnarray}
\bar{y} – \bar{\hat{y}} &=& 
\dfrac{1}{N}(\boldsymbol{y}-\boldsymbol{\hat{y}})^T\boldsymbol{e} \\
&=& 
\dfrac{1}{N}\boldsymbol{\varepsilon}^T\boldsymbol{e} \\
&=& 0
\end{eqnarray}
[/math]

ハイパーパラメタ

重回帰は学習アルゴリズムの挙動を制御するハイパーパラメタはなくパラメタチューニングは不要です。

計算量

回帰係数の算出は

  • 行列[math]\boldsymbol{X}^T\boldsymbol{X}[/math]の計算: [math]O(NP^2)[/math]
  • 逆行列[math]\left(\boldsymbol{X}^T\boldsymbol{X}\right)^{-1}[/math]の計算: [math]O(P^3)[/math]
  • [math]\left(\boldsymbol{X}^T\boldsymbol{X}\right)^{-1}\boldsymbol{X}^T\boldsymbol{y}[/math]の計算: [math]O(NP^2)[/math]

でできるので[math]O(NP^2)[/math]の計算量でできます。

予測時は[math]\boldsymbol{\beta}^T \boldsymbol{x}[/math]を計算するだけなので[math]O(P)[/math]で計算できます。まとめると

重回帰は

  • 学習: [math]O(NP^2)[/math]
  • 予測: [math]O(P)[/math]

でモデルの学習および予測ができる。

データ数と説明変数の数の二乗に比例した計算量で学習し、説明変数の数に比例した計算量で予測できる非常に高速な手法です。

回帰係数が存在するための前提条件の意味

最後に回帰係数が存在するための条件について説明します。回帰係数が存在するには

  1. データ数[math]N[/math]が回帰係数の数[math]P+1[/math]以上であること
  2. [math]{\rm rank}\ \boldsymbol{X}=P+1[/math]

の2つの条件が必要です。

1つ目は求めるパラメタ数以上のデータが必要ということを言っており妥当な前提です。

2つ目は入力データが一次独立であること、つまり各説明変数は他の説明変数の線型結合で表現できないことを要求しています。

例えば「温度（摂氏）[math]T_C[/math]」と「温度（カ氏）[math]T_F[/math]」を同時に説明変数に入れると[math]T_F=\frac{9}{5}T_C+32[/math]という関係があるので

[math]
\begin{eqnarray}

y &=& \beta_F T_F + \beta_C T_C + \beta_0 \\
&=& (\beta_F – 1)T_F + \left(\beta_C + \frac{9}{5}\right)T_C + \beta_0 + 32 \\
&=& (\beta_F – 2)T_F + \left(\beta_C + \frac{18}{5}\right)T_C + \beta_0 + 64 \\
&=& \cdots
\end{eqnarray}
[/math]

と目的変数に対する影響を1つに決められず回帰係数を決めることができなくなります。

重回帰では説明変数が一次独立であっても説明変数間に強い相関があると

  • 数値的に不安定
  • 回帰係数の信頼性が低下

などの問題が生じ「多重共線性」と呼ばれます。「多重共線性」は重回帰を使う上での大きな課題の一つなので記事を改めて説明したいと思います。

シリーズ記事

「機械学習」の「教師あり学習手法」の中で最も基本的な手法として「重回帰」の性質を紹介しています。

誤差項について「無相関で分散一定」「独立同一な正規分布」を仮定するとで様々な性質を導くことができますが、ここでは誤差項について特に仮定せずに導ける性質として

  • 考え方と基本的な性質（本記事）: 回帰係数の導出、回帰超平面の性質、計算量との関係
  • 幾何学的な解釈: 重回帰の性質を幾何的に導出
  • 決定係数: 決定係数と相関係数の関係
  • 多重共線性

を解説しています。

また行列やベクトル演算が多く何をしているか理解しづらいと感じた方は説明変数が1つの場合である「単回帰」も参照ください。

スポンサーリンク

関連記事

コメントを残す

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です