単回帰係数の確率分布と有意性検定

誤差項が独立同一な正規分布に従う場合、最小二乗推定量[math]\hat{\beta}_0, \hat{\beta}_1[/math]が従う確率分布を求めることができます。ここでは

• [math]\hat{\beta}_0, \hat{\beta}_1[/math]が正規分布に従うこと
• [math]t[/math]分布使った回帰係数の検定を導けること

を示します。

確率モデル

ここでは目的変数[math]Y_i[/math]と説明変数[math]x_i[/math]の間に

[math]
Y_i = \beta_0 + \beta_1 x_i + \varepsilon_i,\quad i=1,\dots,N
[/math]

の関係があり誤差項[math]\varepsilon_i[/math]は独立で同一の正規分布[math]\mathcal{N}(0, \sigma^2)[/math]に従うと仮定します。

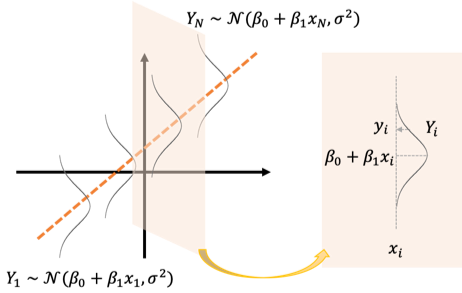
確率変数[math]Y_i[/math]の観測値を[math]y_i[/math]とします。確率モデルは何が確率変数で何が確定値なのかわかりにくいので改めてまとめると

• [math]x_i,\ y_i[/math]: 既知の確定値
• [math]\beta_0,\ \beta_1,\ \sigma^2[/math]: 未知の確定値
• [math]Y_i,\ \varepsilon_i[/math]: 確率変数

になります。

最小二乗推定量[math]\hat{\beta}_0, \hat{\beta}_1[/math]が従う確率分布

まず[math]Y_i[/math]が独立な正規分布に従う確率変数であることと「ガウス・マルコフの定理」で紹介した通り[math]\hat{\beta}_0, \hat{\beta}_1[/math]は[math]\sum c_iY_i[/math]の形でかけるので正規分布に従います。また不偏性より

• [math]\hat{\beta}_0[/math]: 平均[math]\beta_0[/math], 分散[math]V[\hat{\beta}_0][/math]の正規分布
• [math]\hat{\beta}_1[/math]: 平均[math]\beta_1[/math], 分散[math]V[\hat{\beta}_1][/math]の正規分布

に従うことが分かります。以下、分散[math]V[\hat{\beta}_0][/math], [math]V[\hat{\beta}_1][/math]を求めます。

[math]\hat{\beta}_1[/math]の分散

まず

• [math]\bar{x}=\frac{1}{N}\sum_{i}x_i[/math]
• [math]\bar{Y}=\frac{1}{N}\sum_{i}Y_i[/math]
• [math]S_{xx} = \sum_i (x_i – \bar{x})^2[/math]

として最小二乗推定量[math]\hat{\beta}_1=\dfrac{1}{S_{xx}}\sum_{i=1}^N (x_i-\bar{x})Y_i[/math]の分散は[math]Y_i[/math]が独立なので

[math]
\begin{eqnarray}

V[\hat{\beta}_1] &=& \dfrac{1}{S_{xx}^2}V\left[\sum_{i=1}^N(x_i-\bar{x})Y_i\right] \\
&=& \dfrac{1}{S_{xx}^2}\sum_{i=1}^N(x_i-\bar{x})^2V[Y_i] \\
&=& \dfrac{1}{S_{xx}^2}\cdot S_{xx}\sigma^2 \\
&=& \dfrac{\sigma^2}{S_{xx}}
\end{eqnarray}
[/math]

になります。

[math]\hat{\beta}_0[/math]の分散

まず[math]\hat{\beta}_0=\bar{Y} – \hat{\beta}_1\bar{x}[/math]を[math]\sum_{i=1}^N c_iY_i[/math]の形に整理すると

[math]
\begin{eqnarray}

\hat{\beta}_0 = \sum_{i=1}^N\left(\dfrac{1}{N} – \dfrac{(x_i-\bar{x})\bar{x}}{S_{xx}}\right) Y_i
\end{eqnarray}
[/math]

になるので

[math]
\begin{eqnarray}

V[
\hat{\beta}_0] = \sigma^2\sum_{i=1}^N\left(\dfrac{1}{N} – \dfrac{(x_i-\bar{x})\bar{x}}{S_{xx}}\right)^2
\end{eqnarray}
[/math]

となります。ここで

[math]
\begin{eqnarray}

&& \sum_{i=1}^N\left(\dfrac{1}{N} – \dfrac{(x_i-\bar{x})\bar{x}}{S_{xx}}\right)^2 \\
&=& \sum_{i=1}^N\left(\dfrac{1}{N^2} – \dfrac{2(x_i-\bar{x})\bar{x}}{NS_{xx}} + \dfrac{(x_i-\bar{x})^2\bar{x}^2}{S_{xx}^2}\right) \\
&=& \left(\dfrac{1}{N} + \dfrac{\bar{x}^2}{S_{xx}}\right)
\end{eqnarray}
[/math]

と整理でき、さらに

[math]
\begin{eqnarray}
S_{xx} &=& \sum_{i=1}^N (x_i – \bar{x})^2 \\
&=& \sum_{i=1}^N (x_i^2 – 2x_i\bar{x} + \bar{x}^2) \\
&=& N\left(\bar{x^2} – \bar{x}^2\right)
\end{eqnarray}
[/math]

より[math]\bar{x}^2=\bar{x^2}-\dfrac{S_{xx}}{N}[/math]なので

[math]

V[
\hat{\beta}_0] = \left(\dfrac{\bar{x^2}}{S_{xx}}\right)\sigma^2
[/math]

になります。

以上より最小二乗推定量[math]\hat{\beta}_0, \hat{\beta}_1[/math]は

• [math]\hat{\beta}_0[/math]: 平均[math]\beta_0[/math], 分散[math]\left(\dfrac{\bar{x^2}}{S_{xx}}\right)\sigma^2[/math]の正規分布
• [math]\hat{\beta}_1[/math]: 平均[math]\beta_1[/math], 分散[math]\dfrac{\sigma^2}{S_{xx}}[/math]の正規分布

に従います。

回帰係数[math]\hat{\beta}_0, \hat{\beta}_1[/math]の検定

[math]\hat{\beta}_0, \hat{\beta}_1[/math]が正規分布に従うことが分かりましたが、未知のパラメタ[math]\sigma^2[/math]を含むためそのままでは検定や推定に使うことができません。

分散[math]\sigma^2[/math]を代替する統計量として最尤推定量[math]\hat{\sigma}^2[/math]が考えられますが、その期待値^[1]一般化して重回帰分析を考えた方が見通しよく期待値を計算できます。詳細はこちらの記事を参照ください。は

[math]

E\left[\hat{\sigma}^2\right] = \dfrac{N-2}{N}\sigma^2
[/math]

と不偏性が成立しません。そこで以下の不偏推定量[math]S^2[/math]

[math]
\begin{eqnarray}


S^2 &=& \dfrac{N}{N-2}\hat{\sigma}^2 \\
&=& \dfrac{1}{N-2}\sum_{i=1}^N\left(Y_i – \hat{\beta}_0 – \hat{\beta}_1 x_i\right)^2
\end{eqnarray}
[/math]

を分散の代わりに使います。この時、以下の命題が成立します。

証明は一般化して重回帰分析を考え、行列演算を使った方が見通しよく議論ができるのでここでは割愛します。詳細を知りたい方は「回帰係数の確率分布」を参照ください。

この命題より[math]\hat{\beta}_0[/math]については統計量[math]T_{\beta_0}[/math]が

[math]
\begin{eqnarray}

T_{\beta_0} &=& \dfrac{\frac{\hat{\beta}_0 – \beta_0}{\sqrt{\bar{x^2}/S_{xx}\sigma^2}}}{\sqrt{\frac{(N-2)S^2}{\sigma^2}\cdot \frac{1}{N-2}}} \\
&=& \dfrac{\hat{\beta}_0 – \beta_0}{\sqrt{\bar{x^2}S^2 / S_{xx}}} \sim t_{N-2}
\end{eqnarray}
[/math]

自由度[math]N-2[/math]の[math]t[/math]分布に従い、[math]\hat{\beta}_1[/math]についても統計量[math]T_{\beta_1}[/math]が

[math]
\begin{eqnarray}


T_{\beta_1} &=& \dfrac{\frac{\hat{\beta}_1 – \beta_1}{\sqrt{\sigma^2 / S_{xx}}}}{\sqrt{\frac{(N-2)S^2}{\sigma^2}\cdot \frac{1}{N-2}}} \\
&=& \dfrac{\hat{\beta}_1 – \beta_1}{\sqrt{S^2/S_{xx}}}\sim t_{N-2}
\end{eqnarray}
[/math]

自由度[math]N-2[/math]の[math]t[/math]分布に従うことが分かります。なお、この分母を[math]\hat{\beta}_1[/math]の標準誤差(Standard Error)と呼び[math]s.e.(\hat{\beta}_1)[/math]と表記します。

[math]

s.e.(\hat{\beta}_1) = \sqrt{\dfrac{S^2}{S_{xx}}}
[/math]

回帰係数の有意性検定

回帰モデルを作る目的の1つは

説明変数[math]x[/math]が目的変数[math]y[/math]の予測に寄与するかどうか

を明らかにすることです。予測に寄与しない場合、[math]\beta_1=0[/math]になると考えられるので

• 帰無仮説[math]H_0[/math]: [math]\beta_1=0[/math]
• 対立仮説[math]H_1[/math]: [math]\beta_1\ne 0[/math]

を適当な有意水準[math]\alpha[/math]で検定し寄与の有無を判断できます。この検定を「回帰係数の有意性検定」と呼びます。

回帰係数[math]\hat{\beta}_1[/math]の有意性検定の手順は以下になります。

1. 事前に有意水準[math]\alpha[/math]を決め棄却域[math]R = \left\{t\ |\ |t-0| > t_{N-2, \alpha/2} \right\}[/math]を求める
2. 統計量[math]

T_{\beta_1}=\dfrac{\hat{\beta}_1 – 0}{\sqrt{S^2/S_{xx}}}[/math]を計算する
3. [math]T_{\beta_1} \in R[/math]ならば帰無仮説を棄却し、そうでないなら帰無仮説を採択する

参考文献

• Casella, G and Berger, R.L.(1990), Statistical Inference(Second Edition): Section 11.3.4 Estimation and Testing with Normal Errors

シリーズ記事

「機械学習」の「教師あり学習手法」の中で最も基本的な手法として「単回帰」の性質を紹介しています。

ここでは誤差項が「独立同一な正規分布」に従うと仮定すると導ける性質として

• 最尤推定量: 最尤推定量は最小二乗推定量と一致
• 誤差の正規性チェック
• 回帰係数の有意性（本記事）: 最小二乗推定量の確率分布と有意性検定を導出
• 信頼区間: 真の値の推定値が従う確率分布から信頼区間を導出
• 予測区間: 観測値が従う確率分布から予測区間を導出

を解説しています。

また単回帰を拡張した「重回帰」でも同様の性質を示せるのでそちらも参照ください。